Розглянемо рівновагу вантажу Р 1 в напрямку осі Ох (рис. 7.6,б), прийнявши  :
:
 , (7.9)
, (7.9)
де 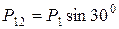 ; Т 1 - сила натягу троса;
; Т 1 - сила натягу троса;
 - сила тертя.
- сила тертя.
З рівняння (7.9) отримаємо
 кН.
кН.
За величиною 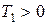 , отже при відсутності троса вантаж Р 1 не буде знаходитися у стані рівноваги, тому що при куті
, отже при відсутності троса вантаж Р 1 не буде знаходитися у стані рівноваги, тому що при куті  умова рівновагі тіла
умова рівновагі тіла  не виконується.
не виконується.
Вантаж Р 1 з’єднано тросом з вантажем Р 2, тому його стан спокою можна забезпечити за допомогою вантажу Р 2, якщо для сили тертя  останнього буде виконуватись нерівність
останнього буде виконуватись нерівність
 кН.
кН.
Величину сили тертя  визначимо, якщо розв’яжемо рівняння рівноваги тіла Р 2 у проекціях на вісь Ох (рис. 7.6,в):
визначимо, якщо розв’яжемо рівняння рівноваги тіла Р 2 у проекціях на вісь Ох (рис. 7.6,в):
 , (7.10)
, (7.10)
де Т 2 = Т 1;  .
.
З (7.10) буде:  (кН). Отже для заданих механічних і геометричних параметрів систем двох тіл отримано, що сила тертя
(кН). Отже для заданих механічних і геометричних параметрів систем двох тіл отримано, що сила тертя  вантажу Р 2 задовольняє умові його рівноваги за наявності нерівної нулю сили натягу троса від вантажу Р 1. Її величина є достатньою для забезпечення особистої рівноваги, а також утримання у спокої і тіла Р 1, тобто рівноваги системи двох тіл в цілому.
вантажу Р 2 задовольняє умові його рівноваги за наявності нерівної нулю сили натягу троса від вантажу Р 1. Її величина є достатньою для забезпечення особистої рівноваги, а також утримання у спокої і тіла Р 1, тобто рівноваги системи двох тіл в цілому.
З рівнянь (7.9), (7.10) можна визначити кут a, при якому матиме стан граничної рівноваги системи вантажів:

або  ,
,
або  . (7.11)
. (7.11)
Формулу (7.11) використовують на практиці при побудові розглянутої на рис. 7.6,а механічної конструкції: визначенні геометричних і механічних параметрів опорної поверхні, вантажів та ін.
Приклад 2. Тертя кочення.
Визначити значення кута  (рис. 7.7), при якому циліндр вагою Р і радіусом R = 5 см знаходиться на похилій шорсткій площині у граничній рівновазі при коченні, якщо f 0 = 0,1; а d = 0,05 см.
(рис. 7.7), при якому циліндр вагою Р і радіусом R = 5 см знаходиться на похилій шорсткій площині у граничній рівновазі при коченні, якщо f 0 = 0,1; а d = 0,05 см.

Рис. 7.7

 :
: , (7.9)
, (7.9)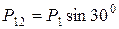 ; Т 1 - сила натягу троса;
; Т 1 - сила натягу троса; - сила тертя.
- сила тертя. кН.
кН.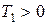 , отже при відсутності троса вантаж Р 1 не буде знаходитися у стані рівноваги, тому що при куті
, отже при відсутності троса вантаж Р 1 не буде знаходитися у стані рівноваги, тому що при куті  умова рівновагі тіла
умова рівновагі тіла  не виконується.
не виконується. останнього буде виконуватись нерівність
останнього буде виконуватись нерівність кН.
кН. , (7.10)
, (7.10) .
. (кН). Отже для заданих механічних і геометричних параметрів систем двох тіл отримано, що сила тертя
(кН). Отже для заданих механічних і геометричних параметрів систем двох тіл отримано, що сила тертя  вантажу Р 2 задовольняє умові його рівноваги за наявності нерівної нулю сили натягу троса від вантажу Р 1. Її величина є достатньою для забезпечення особистої рівноваги, а також утримання у спокої і тіла Р 1, тобто рівноваги системи двох тіл в цілому.
вантажу Р 2 задовольняє умові його рівноваги за наявності нерівної нулю сили натягу троса від вантажу Р 1. Її величина є достатньою для забезпечення особистої рівноваги, а також утримання у спокої і тіла Р 1, тобто рівноваги системи двох тіл в цілому.
 ,
, . (7.11)
. (7.11) (рис. 7.7), при якому циліндр вагою Р і радіусом R = 5 см знаходиться на похилій шорсткій площині у граничній рівновазі при коченні, якщо f 0 = 0,1; а d = 0,05 см.
(рис. 7.7), при якому циліндр вагою Р і радіусом R = 5 см знаходиться на похилій шорсткій площині у граничній рівновазі при коченні, якщо f 0 = 0,1; а d = 0,05 см.



