Способи визначення координат центра ваги
1. Спосіб симетрії. Якщо однорідне тіло має площину, вісь або центр симетрії, то його центр ваги знаходиться відповідно в площині, на осі або в центрі симетрії.
цих точок збігаються координати
Розглянувши всі елементарні об’єми, отримаємо:
і обчислимо координату
Це означає, що центр ваги розглядуваного тіла знаходиться у площині симетрії. Аналогічно можна довести твердження для тіла, що має вісь або центр симетрії. Приклади. Розглянемо декілька прикладів.
(рис. 9.8). Як відомо, діагоналі в точці перетину діляться навпіл.
2. Спосіб розбиття. Якщо тіло можна розбити на скінченне число таких часток, для яких положення центрів ваги відомі, то координати центра ваги тіла можна обчислити за формулами (9.10), (9.12), (9.14) або (9.17). Приклад 1. Визначити координати центра ваги площі (рис. 9.10).
Рис. 9.10 | Розв’язання. Розіб’ємо площу на два прямокутники, центри ваги яких С 1 і С 2 знаходяться в точках перетину діагоналей. Виберемо систему координат Оху. Дані про координати центрів ваги прямокутників і їх площі запишемо в табл. 9.1. |
Таблиця 9.1
| k | xk | yk | Sk |
| 1,5 a | 4 a | 6 a 2 | |
| 2,5 a | 1,5 a | 15 a 2 |
Координати центра ваги площі знайдемо за формулами (9.14):
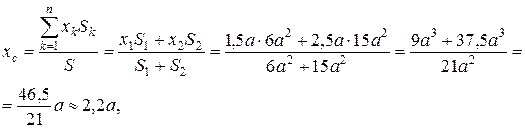

Значення координат точки С (2,2 а; 2,2 а) свідчать, що вона лежить на бісектрисі кута, проведеної з центра координат, яка є лінією симетрії площі.
3. Спосіб доповнення (або від’ємних площин). Якщо тіло має порожнину (виріз), то цю порожнину (виріз) можна розглядати як тіло з від’ємною вагою (площею) і для розрахунків використовувати спосіб розбиття.
Приклад 2. Розглянемо задачу прикладу 1.
   Рис. 9.11
Рис. 9.11
| Розв’язання. Уявимо площу як квадрат (1) зі сторонами 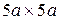 , з якого вирізали квадрат (2) зі сторонами , з якого вирізали квадрат (2) зі сторонами 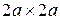 (рис. 9.11). Площу останнього квадрата будемо вважати від’ємною. Дані про координати центрів ваги квадратів і їх площі запишемо в табл. 9.2. (рис. 9.11). Площу останнього квадрата будемо вважати від’ємною. Дані про координати центрів ваги квадратів і їх площі запишемо в табл. 9.2.
|
Таблиця 9.2
| k | xk | yk | Sk |
| 2,5 a | 2,5 a | 25 a 2 | |
| 4 a | 4 a | -4 a 2 |
Координати центра ваги площі знайдемо за формулами (9.14):

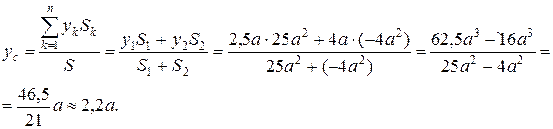
4. Спосіб інтегрування. Якщо тіло неможливо розбити на скінченне число часток, у формулах (9.10), (9.12), (9.14), (9.17) переходять до інтегралів.
Наприклад, формули (9.14) матимуть вигляд:
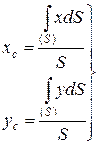 , (9.18)
, (9.18)
де інтеграли поширюються на площу  .
.

 Рис. 9.6
Рис. 9.6
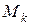 і
і  , які розташовані симетрично відносно площини хОу. У
, які розташовані симетрично відносно площини хОу. У
 , а координати
, а координати  розрізняються тільки знаком. Виділимо навколо точок
розрізняються тільки знаком. Виділимо навколо точок  . Підсумуємо додатки:
. Підсумуємо додатки: .
.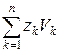 = 0
= 0 центра ваги тіла за формулою (9.12):
центра ваги тіла за формулою (9.12): .
. Рис. 9.7
Рис. 9.7
 Рис. 9.8
Рис. 9.8
 в) коло
Рис. 9.9
в) коло
Рис. 9.9




