Порядок розрахунку простої ферми
1. Спочатку складають три рівняння рівноваги для визначення реакцій опор ферми, розглядаючи останню в цілому як тверде тіло. Після визначення реакцій бажано скласти перевірочне рівняння. Формально умови рівноваги вузлів ферми включають у себе умови рівноваги ферми в цілому, тобто дають змогу знайти і реакції опор. Але попереднє визначення опорних реакцій суттєво спрощує розв’язання задачі. 2. Далі визначають зусилля у стержнях ферми. Звичайно використовують два способи: вирізання вузлів і Ріттера. а) Спосіб вирізання вузлів. Цим способом зручно користуватись, коли треба знайти зусилля в усіх стержнях ферми. Він зводиться до послідовного розгляду умов рівноваги збіжних систем сил, прикладених до кожного з вузлів. При цьому кількість невідомих зусиль у вузлі не повинна перевищувати двох. Для визначеності припускають, що всі зусилля направлені від вузла, тобто стержні розтягнуті. Якщо в результаті розрахунків значення зусилля буде від’ємним, то це означатиме, що стержень стиснутий. Останній вузол розглядають, як правило, для перевірки. Зусилля в окремих стержнях можуть виявитись нульовими, тобто стержні будуть ненавантаженими. Такі стержні можна визначити за допомогою кількох лем.
 Лема 1. Якщо в ненавантаженому вузлі ферми збігаються два стержні (рис. 8.8), то зусилля в цих стержнях дорівнюватимуть нулю, тобто Лема 1. Якщо в ненавантаженому вузлі ферми збігаються два стержні (рис. 8.8), то зусилля в цих стержнях дорівнюватимуть нулю, тобто
 і і 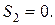
 . .
  Рис. 8.9 Рис. 8.9
Рис. 8.10 б) Спосіб Ріттера. Цим способом зручно користуватись, коли треба знайти зусилля в окремих стержнях ферми, зокрема, для перевірочних розрахунків. Згідно з цим способом ферму розподіляють на дві частини перерізом, який проходить не більше, ніж через три стержні, і розглядають рівновагу однієї з частин. Зусилля в перерізаних стержнях направляють від перерізу, тобто припускають (як і в способі вирізання вузлів), що всі стержні розтягнуті. Далі складають рівняння рівноваги так, щоб у кожне рівняння увійшло тільки одне зусилля стержня, через який пройшов переріз. Для цього складають рівняння моментів відносно точки площини (цю точку називають точкою Ріттера), через яку проходять лінії дій зусиль двох інших стержнів, які потрапили в переріз. Якщо два інших стержні перерізу виявляються паралельними, то складають рівняння проекцій сил на вісь, яка перпендикулярна до цих паралельних стержнів. Таким чином, спосіб Ріттера хдає змогу визначить зусилля в будь-якому стержні ферми незалежно від зусиль в інших стержнях. Аналізуючи вищеназвані способи визначення зусиль у стержнях, зазначимо, що зусилля способом вирізання вузлів визначають послідовно, переходячи від одного вузла до сусіднього. Це може призвести до накопичення похибок, тому бажано значення знайдених зусиль при розгляді наступних вузлів брати якомога точнішими. Крім того, помилка у визначенні одного зусилля призведе до неправильних розрахунків усіх інших стержнів, що залишились. Спосіб Ріттера на відміну від попереднього не призводить до накопичення похибок, бо всі зусилля визначаються незалежно одне від одного. Але одночасно це не дає можливості помітити грубі помилки, що можуть трапитись при обчисленні. У деяких фермах також не всі зусилля можуть бути визначені способом Ріттера незалежно одне від одного. Таким чином, найкраща методика визначення зусиль у стержнях ферми полягає в поєднанні способів вирізання вузлів і Ріттера. При цьому всі зусилля визначаються за способом вирізання вузлів і деякі з них перевіряють способом Ріттера. Приклад 1. Визначити зусилля у стержнях ферми (рис. 8.11), на яку діє задана сила
Розв’язання: 1) Розглянемо рівновагу ферми (рис. 8.12) і визначимо реакції опор А і В:
де
Перевірка:
2) Визначимо зусилля у стержнях ферми методом вирізання вузлів: а) розглянемо рівновагу вузла А (рис. 8.13):
(за модулем
друге рівняння можна використати для перевірки:
(
(
Відповідь: 1) XA» -7 кН; YA» -7 кН; RB= 14 кН; знаки «-» означають, що справжнє направлення складових 2) S1 = 10 кН; S2 = 0; S3 = -10 кН; S4 » 14 кН; S5 = -10 кН; стержні 1, 4 - розтягнуті; 3, 5 - стиснуті; 2 - ненавантажений.
|

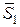
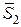
 Рис. 8.8
Рис. 8.8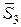

 Лема 3. Якщо до вузла, в якому збігаються два стержні, прикладена зовнішня сила
Лема 3. Якщо до вузла, в якому збігаються два стержні, прикладена зовнішня сила 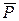 у напрямку одного з стержнів (рис. 8.10), то зусилля у другому стержні дорівнює нулю:
у напрямку одного з стержнів (рис. 8.10), то зусилля у другому стержні дорівнює нулю:  .
.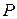 = 10 кН. Зусилля у стержнях 2, 3, 4 перевірити способом Ріттера.
= 10 кН. Зусилля у стержнях 2, 3, 4 перевірити способом Ріттера.

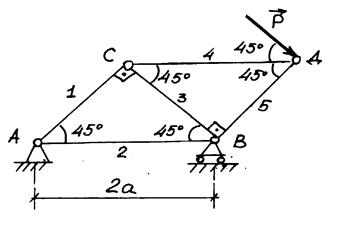 Рис. 8.11
Рис. 8.11
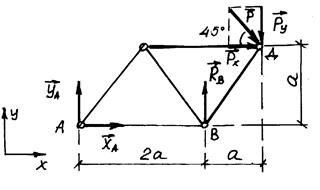 Рис. 8.12
Рис. 8.12
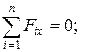

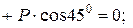
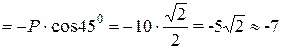 (кН)
(кН)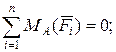
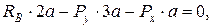
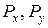 - модулі складових сили
- модулі складових сили 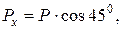
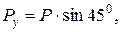
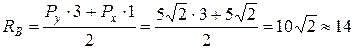 кН;
кН;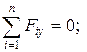
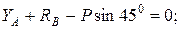
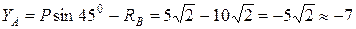 (кН).
(кН).


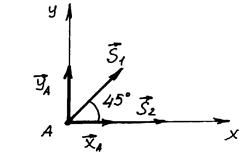 Рис. 8.13
Рис. 8.13
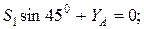
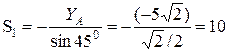 (кН);
(кН);





 (кН);
(кН);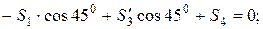
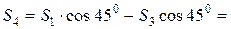
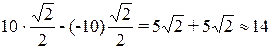 (кН);
(кН);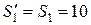 кН);
кН);
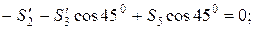


 Рис. 8.15
Рис. 8.15
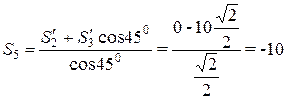 (кН);
(кН);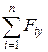 =
= 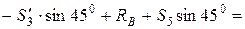
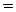

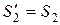 ;
; 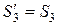 );
);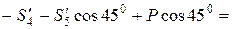


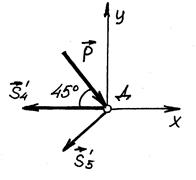 Рис. 8.16
Рис. 8.16
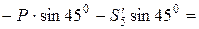
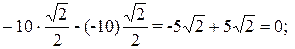
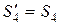 ;
; 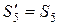 );
);






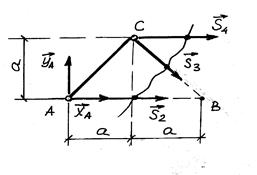 Рис. 8.17
Рис. 8.17
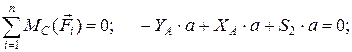
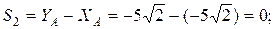
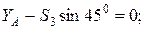
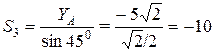 (кН);
(кН);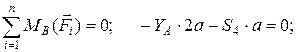
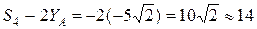 (кН).
(кН). протилежне показаним на рисунках;
протилежне показаним на рисунках;


