Розв’язання. Складемо рівняння рівноваги циліндра
Складемо рівняння рівноваги циліндра:
де З другого рівняння системи (7.12) отримаємо
звідкиля отже, З першого рівняння маємо
Отже, враховуючи, що сила тертя в умові граничної рівноваги циліндра при коченні (коли Розрахунок плоскої ферми Основні визначення і припущення Фермою називається геометрично незмінна конструкція, що складається з прямолінійних стержнів, які з’єднуються між собою за допомогою шарнірів. Ферми являють собою досить розповсюджені складові частини промислових і цивільних споруд. Їх використовують як опори трубопроводів і ліній електропередач (рис. 8.1), радіовежі (рис. 8.2), конструкції кранів, елементи великих прольотів будівельних та спортивних споруд, елементи мостів (рис. 8.3, 8.4, 8.5) та ін.
Якщо всі стержні ферми розташовані в одній площині, ферму називають плоскою. З’єднання стержнів ферми між собою називається вузлами.
Рис. 8.3. Мостова ферма
Рис. 8.4. Елемент даху спортивного залу в Парижі (Франція)
Рис. 8.5. Залізничний міст в Единбурзі (Шотландія)
Основним завданням розрахунку ферми є визначення зусиль, що виникають у стержнях при дії зовнішнього навантаження. При цьому розрахунки виконують при наступних припущеннях: - усі зовнішні навантаження прикладені тільки у вузлах; - вагою стержнів і тертям у вузлах, які є ідеальними шарнірами, нехтують.
Рис. 8.7
Розглянемо зв’язок між кількістю вузлів п і кількістю стержнів k у простих фермах. Основний трикутник (рис. 8.6) має три вузли і три стержні. Для незмінного з’єднання з основним трикутником кожного з решти п -3 вузлів потрібно приєднати два стержні. Отже, загальна кількість стержнів у простої ферми з урахуванням трьох стержнів основного трикутника визначається так:
Покажемо, що проста ферма статично означена, якщо число опорних реакцій дорівнює трьом. Дійсно, для кожного вузла можна скласти два рівняння рівноваги, оскільки на нього діє збіжна система сил. Таким чином, усього можна скласти 2 п рівнянь рівноваги. У ці рівняння будуть входити k невідомих зусиль у стержнях і три реакції опор. З урахуванням формули (8.1) загальне число невідомих буде:
тобто дорівнюватиме числу рівнянь рівноваги. Таким чином, задачу розрахунку простих ферм можна розв’язати методами теоретичної механіки. Зазначимо, що якщо число стержнів k менше, ніж підраховане за формулою (8.1), то така конструкція буде механізмом, тобто матиме можливість рухатися. Якщо число стержнів більше, ніж підраховане за формулою (8.1), або число опорних реакцій більше трьох, ферма буде статично неозначена і для її розрахунку треба застосувати методи будівельної механіки.
|

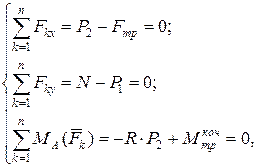 (7.12)
(7.12) - нормальна складова реакції площини;
- нормальна складова реакції площини;  - момент тертя кочення циліндра. При рівновазі циліндра буде виконуватись
- момент тертя кочення циліндра. При рівновазі циліндра буде виконуватись 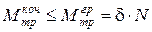 .
. . Тоді третє рівняння в умовах граничної рівноваги набуде вигляду
. Тоді третє рівняння в умовах граничної рівноваги набуде вигляду ,
, ,
, .
. . Для зображеної на рис. 7.7 механічної схеми максимальна величина сили тертя спокою
. Для зображеної на рис. 7.7 механічної схеми максимальна величина сили тертя спокою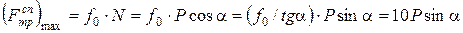 .
. ) задовольняє нерівності
) задовольняє нерівності  , по площині циліндр ковзати не буде.
, по площині циліндр ковзати не буде. Рис. 8.1. Опори ЛЕП
Рис. 8.1. Опори ЛЕП
 Рис. 8.2. Ейфелева вежа
(Париж, Франція)
Рис. 8.2. Ейфелева вежа
(Париж, Франція)



 Тоді на підставі першої аксіоми статики можна вважати, що стержні ферми працюють тільки на розтяг або стиск. Наведені припущення вносять певну похибку в розрахунки у порівнянні з дійсним напруженим станом стержнів, але ця похибка невелика і отримані результати можна використовувати для технічних розрахунків елементів ферми на міцність.
Тоді на підставі першої аксіоми статики можна вважати, що стержні ферми працюють тільки на розтяг або стиск. Наведені припущення вносять певну похибку в розрахунки у порівнянні з дійсним напруженим станом стержнів, але ця похибка невелика і отримані результати можна використовувати для технічних розрахунків елементів ферми на міцність.

 Простою плоскою фермою називається ферма, яка може бути побудована з трикутної шляхом послідовного приєднання кожного нового вузла за допомогою двох нових стержнів (рис. 8.7).
Простою плоскою фермою називається ферма, яка може бути побудована з трикутної шляхом послідовного приєднання кожного нового вузла за допомогою двох нових стержнів (рис. 8.7).
 . (8.1)
. (8.1) ,
,


