Розглянемо декілька простих фігур, з яких можуть складатись більш складні фігури.
 а) трикутник а) трикутник
Рис. 9.12
|
Скористаємось способом роз-биття і розділимо трикутник АВД на елементарні смужки, провівши лінії, паралельні стороні АД (рис. 9.12). Кожну таку смужку можна прийняти за прямокутник, центр симетрії якого лежить у середині, тобто на медіані ВК
|
трикутника. Розглядаючи смужки, паралельні стороні ВД, приходимо до висновку, що центр ваги трикутника має лежати на медіані AL. Отже, центр ваги трикутника знаходиться у точці перетину його медіан. Ця точка, як відомо, ділить кожну із медіан у відношенні 1:2, тобто 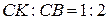 ,
,  .
.
 б) дуга кола
б) дуга кола
Рис. 9.13
Розглянемо дугу АВ кола радіусом R з центральним кутом  (рис. 9.13). Направимо вісь Ох по осі симетрії дуги, яка є бісектрисою кута
(рис. 9.13). Направимо вісь Ох по осі симетрії дуги, яка є бісектрисою кута  . Центр ваги дуги кола лежить на осі симетрії, тобто
. Центр ваги дуги кола лежить на осі симетрії, тобто 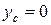 , і залишається знайти
, і залишається знайти  . Для цього скористаємось формулою
. Для цього скористаємось формулою
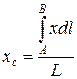 , (9.19)
, (9.19)
яка вийде, якщо у формулі (9.17) перейти до інтеграла. Для елементарної частки довжини  , як виходить з рис. 9.13,
, як виходить з рис. 9.13,  ,
,  ,
,  . Тоді
. Тоді
 . (9.20)
. (9.20)
 в) коловий сектор
в) коловий сектор
Рис. 9.14
Розглянемо коловий сектор з центральним кутом  і радіусом R (рис. 9.14). Направимо вісь Ох по осі симетрії сектора, яка є бісектрисою кута
і радіусом R (рис. 9.14). Направимо вісь Ох по осі симетрії сектора, яка є бісектрисою кута  . Центр ваги сектора лежить на осі симетрії, тобто
. Центр ваги сектора лежить на осі симетрії, тобто 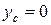 . Розіб’ємо коловий сектор на елементарні сектори (заштрихований на рис. 9.14), кожен з котрих можна прийняти за рівнобедрений трикутник. Отже, центр ваги кожного елементарного трикутника лежить на відстані
. Розіб’ємо коловий сектор на елементарні сектори (заштрихований на рис. 9.14), кожен з котрих можна прийняти за рівнобедрений трикутник. Отже, центр ваги кожного елементарного трикутника лежить на відстані 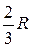 від початку координат. Геометричним місцем центрів ваги всіх елементарних трикутників буде дуга кола радіусом
від початку координат. Геометричним місцем центрів ваги всіх елементарних трикутників буде дуга кола радіусом 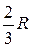 . У цьому випадку можна скористатись формулою для центра ваги дуги кола (9.20):
. У цьому випадку можна скористатись формулою для центра ваги дуги кола (9.20):
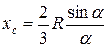 . (9.21)
. (9.21)
Зауваження. У формулах (9.20), (9.21) кут  треба брати в радіанах.
треба брати в радіанах.

 а) трикутник
а) трикутник
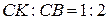 ,
,  .
. б) дуга кола
б) дуга кола (рис. 9.13). Направимо вісь Ох по осі симетрії дуги, яка є бісектрисою кута
(рис. 9.13). Направимо вісь Ох по осі симетрії дуги, яка є бісектрисою кута 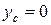 , і залишається знайти
, і залишається знайти  . Для цього скористаємось формулою
. Для цього скористаємось формулою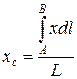 , (9.19)
, (9.19) , як виходить з рис. 9.13,
, як виходить з рис. 9.13,  ,
,  ,
,  . Тоді
. Тоді . (9.20)
. (9.20) в) коловий сектор
в) коловий сектор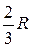 від початку координат. Геометричним місцем центрів ваги всіх елементарних трикутників буде дуга кола радіусом
від початку координат. Геометричним місцем центрів ваги всіх елементарних трикутників буде дуга кола радіусом 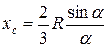 . (9.21)
. (9.21) треба брати в радіанах.
треба брати в радіанах.


