Центр паралельних сил і центр ваги
Центр паралельних сил
Рис. 9.1 |  , ,
 . (9.1)
Якщо сили . (9.1)
Якщо сили  и и  повернути на однаковий кут повернути на однаковий кут  навколо точок їх прикладання А і В, то рівнодійна навколо точок їх прикладання А і В, то рівнодійна 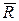 повернеться на той самий кут навколо точки повернеться на той самий кут навколо точки
|
С, оскільки співвідношення (9.1) не зміняться. Такі ж міркування можна привести і для двох паралельних сил, направлених у різні боки.
Точка С, через яку проходить лінія дії рівнодійної системи паралельних сил при будь-яких поворотах цих сил навколо точок їх прикладання на однаковий кут, називається центром паралельних сил.
У яких випадках існує така точка С і як знайти їх координати? На це запитання дає відповідь теорема про центр паралельних сил.
Теорема. Якщо головний вектор системи паралельних сил не дорівнює нулю, то центр паралельних сил (точка С) існує і його положення визначається за формулою
 , (9.2)
, (9.2)
де  - радіуси-вектори точок прикладання сил;
- радіуси-вектори точок прикладання сил;  - радіус-вектор центра паралельних сил;
- радіус-вектор центра паралельних сил;  - модулі паралельних сил, які відрізняються знаком для сил, направлених у різні боки.
- модулі паралельних сил, які відрізняються знаком для сил, направлених у різні боки.
Доведення. Розглянемо систему п паралельних сил  . Якщо її головний вектор не дорівнює нулю, то, як показано у п. 5.4.4.3, така система паралельних сил зводиться до рівнодійної
. Якщо її головний вектор не дорівнює нулю, то, як показано у п. 5.4.4.3, така система паралельних сил зводиться до рівнодійної 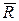 . Нехай точка
. Нехай точка  - це якась точка лінії дії цієї рівнодійної (рис. 9.2),
- це якась точка лінії дії цієї рівнодійної (рис. 9.2),  - відповідно радіуси-вектори точки
- відповідно радіуси-вектори точки  і точок прикладання сил
і точок прикладання сил 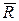 і
і  відносно вибраного центра О.
відносно вибраного центра О.
 Рис. 9.2
Рис. 9.2
| Згідно з теоремою Варіньона про момент рівнодійної (п. 5.6), отримаємо
 або або  або
або  . (9.3)
Рівність (9.3) запишемо у наступній формі . (9.3)
Рівність (9.3) запишемо у наступній формі
|
 . (9.4)
. (9.4)
Введемо у розгляд одиничний вектор  , паралельний лініям дії сил
, паралельний лініям дії сил  . Тоді кожна із заданої системи сил може бути виражена через вектор
. Тоді кожна із заданої системи сил може бути виражена через вектор  :
:
 , (9.5)
, (9.5)
де  , якщо напрями векторів
, якщо напрями векторів  и
и  збігаються, і
збігаються, і  , якщо ці напрями протилежні. При цьому очевидно, що
, якщо ці напрями протилежні. При цьому очевидно, що
 . (9.6)
. (9.6)
Підставляючи (9.5) і (9.6) у рівняння (9.4), отримаємо:
 ,
,
або 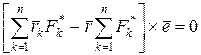 .
.
Остання рівність виконується при будь-якому напрямі сил (напрямі вектора  ) тільки за умовою, що перший множник дорівнює нулю:
) тільки за умовою, що перший множник дорівнює нулю:
 . (9.7)
. (9.7)
Ця рівність має єдиний розв’язок відносно радіуса-вектора  , який визначає точку прикладання рівнодійної. Такою точкою і є центр паралельних сил, чим доводиться його існування. Позначимо радіус-вектор центра паралельних сил як
, який визначає точку прикладання рівнодійної. Такою точкою і є центр паралельних сил, чим доводиться його існування. Позначимо радіус-вектор центра паралельних сил як  . Тоді з рівняння (9.7) отримаємо вираз:
. Тоді з рівняння (9.7) отримаємо вираз:

Теорему доведено.
Формулу (9.2) можна подати у скалярній формі:
 ,
,  ,
,  , (9.9)
, (9.9)
де  - відповідно декартові координати центра с паралельних сил і точок прикладання сил
- відповідно декартові координати центра с паралельних сил і точок прикладання сил  .
.
Вирази  ,
, 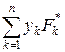 ,
,  у формулах (9.9) називаються відповідно статичними моментами заданої системи сил відносно координатних площин уOz, xOz, xOy. Зазначимо, що коли початок координат сумістити з центром паралельних сил, то
у формулах (9.9) називаються відповідно статичними моментами заданої системи сил відносно координатних площин уOz, xOz, xOy. Зазначимо, що коли початок координат сумістити з центром паралельних сил, то

і статичні моменти заданої системи сил дорівнюватимуть нулю.

 Розглянемо дві паралельні сили
Розглянемо дві паралельні сили 





