Розв’язання.
Розрахункова схема наведена на рис. 6.5,б. При її побудові використано принцип звільнення від в’язів, розподілене навантаження замінено зосередженою силою
а
б Рис. 6.5 Відповідно до рис. 6.5,б, балка як вільне тверде тіло, перебуває в рівновазі під дією заданих сил Складемо рівняння рівноваги балки, використавши першу форму умов рівноваги довільної плоскої системи сил:
З отриманих трьох рівнянь можна визначити три невідомі реакції: з першого рівняння
з другого рівняння
з третього рівняння
Знак (-) отриманої реакції Для перевірки одержаних величин реакцій в’язів складемо рівняння моментів сил відносно точки Е, що знаходиться на відстані 1 м від точки В і від балки (рис.6.5, б). Перевірка.
Приклад 2. Рівновага довільної системи сил у просторі. Початкова схема конструкції (рис. 6.6) складається з вертикального вала АВС вагою
|
кН, а сила 
- координатними складовими 
, 
з величинами
кН,
кН.
, пари сил з моментом 
і реакції защемлення у вигляді силових складових 
та пари сил з моментом 
.
; 
;
; 
;
; 
.
(кН);
(кН);
(кН×м).
показує, що в дійсності вона направлена на розрахунковій схемі у протилежний бік.
.
кН, який розташований у підп’ятнику А і підшипнику В. На валу жорстко закріплено два шківи радіусами 
см і 
см, до яких прикладені колові зусилля 
. Необхідно визначити реакції підп’ятника А, підшипника В і величину колового зусилля 
, які забезпечують рівновагу вала при наступних геометричних і кутових параметрах вала і навантаженнях: 
см; 
см; 
, вектори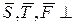 
осі 
; 
кН; 
кН.
