Приклад 1. Для зображеної на рис. 5.26 довільної системи сил 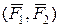 у площині визначити в центрі О головний вектор
у площині визначити в центрі О головний вектор  , головний момент
, головний момент  , параметри рівнодійної
, параметри рівнодійної  вихідної системи сил та її рівняння. Початкові дані:
вихідної системи сил та її рівняння. Початкові дані: 
 ,
, 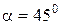 , координати точок прикладання сил:
, координати точок прикладання сил: 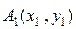 ;
; 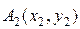 .
.
Рис. 5.26
Розв’язання. Визначимо, враховуючи рівняння (5.2) і (5.3), параметри головного вектора і головного моменту заданої системи сил стосовно центра О:  ,
, 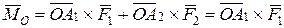 (добуток
(добуток 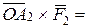 0, тому що вектори
0, тому що вектори  і
і 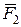 паралельні). Побудуємо вектори
паралельні). Побудуємо вектори  і
і  . При побудові головного вектора
. При побудові головного вектора  використовуємо методику теореми Пуансо: сили
використовуємо методику теореми Пуансо: сили  і
і 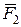 перенесемо в точку О паралельно самим до себе; отримані
перенесемо в точку О паралельно самим до себе; отримані  і
і 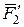 додамо геометрично і результуючу силу визначимо як головний вектор
додамо геометрично і результуючу силу визначимо як головний вектор  вихідної системи сил
вихідної системи сил 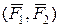 у центрі О.
у центрі О.
Для заданої системи сил у точці О головний момент  , тому його дугову стрілку спрямуємо у бік проти ходу стрілки годинника.
, тому його дугову стрілку спрямуємо у бік проти ходу стрілки годинника.
Проаналізуємо отримані результати.
За величинами  і
і  , тому вихідна плоска система сил зводиться, відповідно до п. 5.5.4, до однієї рівнодійної сили
, тому вихідна плоска система сил зводиться, відповідно до п. 5.5.4, до однієї рівнодійної сили  .
.
Представимо далі момент  (закреслено на рис. 5.26) у вигляді пари сил
(закреслено на рис. 5.26) у вигляді пари сил 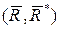 , в якій сила
, в якій сила 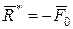 , а плече
, а плече 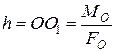 . За визначенням сили
. За визначенням сили  і
і 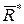 складають двійку сил, тому система сил
складають двійку сил, тому система сил  .
.
Отже вихідну систему сил 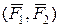 еквівалентними системними перетвореннями
еквівалентними системними перетвореннями
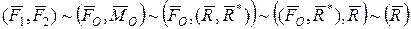
зведено до однієї сили, рівнодійної  з точкою прикладання О 1 на відстані ОО 1 від полюса О в бік додатного відліку координати х. Лінією дії рівнодійної буде пряма з рівнянням
з точкою прикладання О 1 на відстані ОО 1 від полюса О в бік додатного відліку координати х. Лінією дії рівнодійної буде пряма з рівнянням 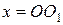 , де
, де  - число.
- число.
Приклад 2. Для зображеної на рис. 5.27,а довільної системи сил  у просторі визначити головний вектор
у просторі визначити головний вектор  , головний момент
, головний момент  , параметри
, параметри  і
і 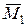 динамічного гвинта і рівняння його осі. Початкові дані: сили
динамічного гвинта і рівняння його осі. Початкові дані: сили 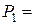 4 Н; Р 2 = 3 Н; відстань ОА = 1 м.
4 Н; Р 2 = 3 Н; відстань ОА = 1 м.
Розв’язання. Визначимо відповідно до теореми Пуансо головний вектор 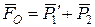 (тут
(тут 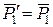 ) і головний момент
) і головний момент  (рис. 5.27,б), а також їх величини і проекції:
(рис. 5.27,б), а також їх величини і проекції:  (Н);
(Н);  Н×м;
Н×м; 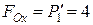 Н,
Н, 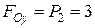 Н;
Н;  ,
,  ,
,  Н×м;
Н×м; 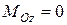 . Кут
. Кут 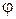 між векторами
між векторами  і
і  дорівнює
дорівнює 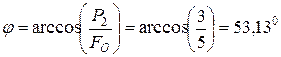 і задовольняє умові
і задовольняє умові 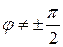 . Тому вихідна система сил зводиться, відповідно до п. 5.4.4.1, до динамічного гвинта. Представимо далі головний момент системи сил у полюсі О (рис. 5.27,б) як
. Тому вихідна система сил зводиться, відповідно до п. 5.4.4.1, до динамічного гвинта. Представимо далі головний момент системи сил у полюсі О (рис. 5.27,б) як 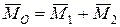 , де
, де 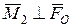 за побудовою. За умовою задачі та за побудовою вектори
за побудовою. За умовою задачі та за побудовою вектори  і
і  ,
, 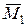 і
і 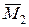 належатимуть площині хОу, а
належатимуть площині хОу, а 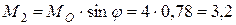 Н×м. Представимо (рис. 5.27,в) момент
Н×м. Представимо (рис. 5.27,в) момент 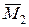 парою сил
парою сил 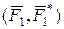 з плечем
з плечем 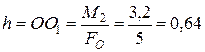 (м) і силою
(м) і силою  .
.
Врахуємо далі, що сили  і
і  складають двійку сил, тобто система сил
складають двійку сил, тобто система сил  , і перенесемо момент
, і перенесемо момент 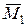 , як вільний вектор, в точку О 1 прикладання сили
, як вільний вектор, в точку О 1 прикладання сили  . У результаті вихідна система сил перетвориться у систему (рис. 5.27,г) двох силових факторів
. У результаті вихідна система сил перетвориться у систему (рис. 5.27,г) двох силових факторів  і
і 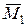 , що складають силу і момент динами.
, що складають силу і момент динами.
а б
в г
Рис. 5.27
Проведені на рис. 5.16,а,б,в еквівалентні векторні перетворення систем сил мають вигляд

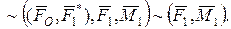
Рівняння осі С 1 С 2 динамічного гвинта у просторі Охуz має вигляд
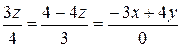 . (5.25)
. (5.25)
Відповідно до (5.25) на рис. 5.27,г вісь динамічного гвинта є перетинанням площин z = 0,64 і 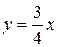 .
.
Під дією динамічного гвинта вільне тверде тіло може здійснювати тільки складний (гвинтовий рух).
Приведення системи сил до динамічного гвинта має важливе значення стосовно задач зрівноваження. Якщо, наприклад, до тіла додати ззовні силу 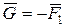 (рівну за величиною і протилежно направлену силі
(рівну за величиною і протилежно направлену силі  ), а у перпендикулярній осі динами площині прикласти пару сил з моментом
), а у перпендикулярній осі динами площині прикласти пару сил з моментом 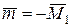 , то зрівноваження тіла буде досягнуто за умов найменшої потужності використаних зовнішніх силових факторів. Силу
, то зрівноваження тіла буде досягнуто за умов найменшої потужності використаних зовнішніх силових факторів. Силу  і момент
і момент  на рис. 5.27,г не показано. Ця властивість має важливе значення особливо в космічній техніці.
на рис. 5.27,г не показано. Ця властивість має важливе значення особливо в космічній техніці.

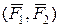 у площині визначити в центрі О головний вектор
у площині визначити в центрі О головний вектор  , головний момент
, головний момент  , параметри рівнодійної
, параметри рівнодійної  вихідної системи сил та її рівняння. Початкові дані:
вихідної системи сил та її рівняння. Початкові дані: 
 ,
, 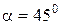 , координати точок прикладання сил:
, координати точок прикладання сил: 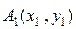 ;
; 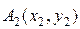 .
. ,
, 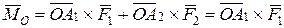 (добуток
(добуток 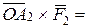 0, тому що вектори
0, тому що вектори  і
і 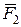 паралельні). Побудуємо вектори
паралельні). Побудуємо вектори  і
і  і
і 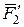 додамо геометрично і результуючу силу визначимо як головний вектор
додамо геометрично і результуючу силу визначимо як головний вектор  , тому його дугову стрілку спрямуємо у бік проти ходу стрілки годинника.
, тому його дугову стрілку спрямуємо у бік проти ходу стрілки годинника. і
і  , тому вихідна плоска система сил зводиться, відповідно до п. 5.5.4, до однієї рівнодійної сили
, тому вихідна плоска система сил зводиться, відповідно до п. 5.5.4, до однієї рівнодійної сили 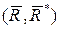 , в якій сила
, в якій сила 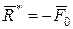 , а плече
, а плече 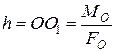 . За визначенням сили
. За визначенням сили 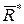 складають двійку сил, тому система сил
складають двійку сил, тому система сил  .
.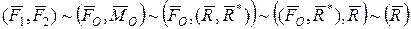
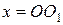 , де
, де  - число.
- число. у просторі визначити головний вектор
у просторі визначити головний вектор 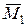 динамічного гвинта і рівняння його осі. Початкові дані: сили
динамічного гвинта і рівняння його осі. Початкові дані: сили 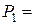 4 Н; Р 2 = 3 Н; відстань ОА = 1 м.
4 Н; Р 2 = 3 Н; відстань ОА = 1 м.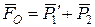 (тут
(тут 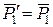 ) і головний момент
) і головний момент  (рис. 5.27,б), а також їх величини і проекції:
(рис. 5.27,б), а також їх величини і проекції:  (Н);
(Н);  Н×м;
Н×м; 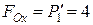 Н,
Н, 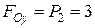 Н;
Н;  ,
,  ,
,  Н×м;
Н×м; 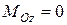 . Кут
. Кут 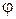 між векторами
між векторами 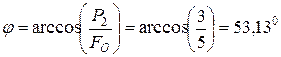 і задовольняє умові
і задовольняє умові 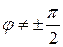 . Тому вихідна система сил зводиться, відповідно до п. 5.4.4.1, до динамічного гвинта. Представимо далі головний момент системи сил у полюсі О (рис. 5.27,б) як
. Тому вихідна система сил зводиться, відповідно до п. 5.4.4.1, до динамічного гвинта. Представимо далі головний момент системи сил у полюсі О (рис. 5.27,б) як 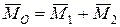 , де
, де 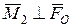 за побудовою. За умовою задачі та за побудовою вектори
за побудовою. За умовою задачі та за побудовою вектори 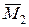 належатимуть площині хОу, а
належатимуть площині хОу, а 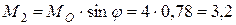 Н×м. Представимо (рис. 5.27,в) момент
Н×м. Представимо (рис. 5.27,в) момент 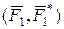 з плечем
з плечем 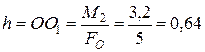 (м) і силою
(м) і силою  .
. складають двійку сил, тобто система сил
складають двійку сил, тобто система сил  , і перенесемо момент
, і перенесемо момент 




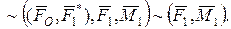
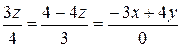 . (5.25)
. (5.25)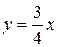 .
.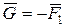 (рівну за величиною і протилежно направлену силі
(рівну за величиною і протилежно направлену силі 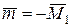 , то зрівноваження тіла буде досягнуто за умов найменшої потужності використаних зовнішніх силових факторів. Силу
, то зрівноваження тіла буде досягнуто за умов найменшої потужності використаних зовнішніх силових факторів. Силу  і момент
і момент  на рис. 5.27,г не показано. Ця властивість має важливе значення особливо в космічній техніці.
на рис. 5.27,г не показано. Ця властивість має важливе значення особливо в космічній техніці.


