На практиці важливе використання, наприклад, при визначенні координат ваги тіла, має наступна властивість головного вектора системи сил (теорема Варіньона про момент рівнодійної).
Теорема. Якщо є точка О, в якій система діючих сил  зводиться тільки до головного вектора
зводиться тільки до головного вектора  , тобто рівнодійної
, тобто рівнодійної  , то момент цієї рівнодійної відносно будь якої іншої точки О 1 дорівнюватиме геометричній сумі моментів сил вихідної системи відносно тієї самої точки О 1.
, то момент цієї рівнодійної відносно будь якої іншої точки О 1 дорівнюватиме геометричній сумі моментів сил вихідної системи відносно тієї самої точки О 1.
При доведенні теореми врахуємо вираз (5.5), а також те, що за умовою в точках О і О 1 на рис. 5.24 вектор  =0.
=0.
У результаті отримаємо:
в точці О 
в точці О 1  ;
;
або  . (5.21)
. (5.21)

Рис. 5.24
Рівняння (5.20) справедливе для будь-якої точки О 1 тіла в просторі чи площині.
Отже теорему доведено.
Особливості використання теореми Варіньона розглянемо на наступних прикладах.
Приклад 1. Для заданої у площині xO1y (рис. 5.25,а) рівнодійної  з точкою прикладання О визначити рівняння лінії її дії.
з точкою прикладання О визначити рівняння лінії її дії.
Розв’язання. Представимо базове рівняння (5.21) теореми Варіньона у вигляді
 , (5.22)
, (5.22)
 де
де  ,
,  - проекції головного вектора
- проекції головного вектора  сил
сил  системи;
системи;  - головний момент системи сил відносно точки О 1
- головний момент системи сил відносно точки О 1  .
.
Рис. 5.25
З (5.22) отримаємо рівняння прямої аа у відрізках
 (5.23)
(5.23)
чи з кутовим коефіцієнтом
 (5.24)
(5.24)
у площині хО 1 у.
Рівняння (5.23) і (5.24) використовують на практиці в будівельній механіці при визначенні, наприклад, параметрів (величин і напрямків дії) реакцій в’язів.
Приклад 2. Визначити момент сили  Н відносно точки О початку системи координат хОу (рис. 5.25, б). Точка прикладання сили має координати А (хА =8 м, уА =10 м), а лінія її дії складає з віссю Ох кут
Н відносно точки О початку системи координат хОу (рис. 5.25, б). Точка прикладання сили має координати А (хА =8 м, уА =10 м), а лінія її дії складає з віссю Ох кут  .
.
Розв’язання. Розкладемо силу 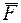 на координатні складові
на координатні складові  і
і  . Визначимо їх величини:
. Визначимо їх величини:  Н,
Н,  Н. За побудовою сила
Н. За побудовою сила 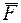 є рівнодійною сил
є рівнодійною сил  і
і  . Тому для знаходження її моменту відносно точки О використаємо теорему Варіньона:
. Тому для знаходження її моменту відносно точки О використаємо теорему Варіньона:

 Н×м.
Н×м.
  б
Рис. 5.25
б
Рис. 5.25
|
тут знак „-” означає, що сила 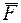 прагне повернути своє плече h за ходом стрілки годинника. прагне повернути своє плече h за ходом стрілки годинника.
|
Примітка. Визначити момент сили  відносно полюса за загальною формулою
відносно полюса за загальною формулою  дуже складно, тому що невідомим є її плече h відносно точки О. Для його визначення спочатку необхідно скласти рівняння (5.23) або (5.24) лінії дії сили. Потім рівняння перпендикуляра з точки О на цю пряму, і далі визначити його довжину, яка і являтиме собою плече h сили
дуже складно, тому що невідомим є її плече h відносно точки О. Для його визначення спочатку необхідно скласти рівняння (5.23) або (5.24) лінії дії сили. Потім рівняння перпендикуляра з точки О на цю пряму, і далі визначити його довжину, яка і являтиме собою плече h сили  відносно полюса О.
відносно полюса О.

 зводиться тільки до головного вектора
зводиться тільки до головного вектора  , тобто рівнодійної
, тобто рівнодійної  , то момент цієї рівнодійної відносно будь якої іншої точки О 1 дорівнюватиме геометричній сумі моментів сил вихідної системи відносно тієї самої точки О 1.
, то момент цієї рівнодійної відносно будь якої іншої точки О 1 дорівнюватиме геометричній сумі моментів сил вихідної системи відносно тієї самої точки О 1. =0.
=0.
 ;
; . (5.21)
. (5.21)
 з точкою прикладання О визначити рівняння лінії її дії.
з точкою прикладання О визначити рівняння лінії її дії. , (5.22)
, (5.22) де
де  ,
,  - проекції головного вектора
- проекції головного вектора  системи;
системи;  - головний момент системи сил відносно точки О 1
- головний момент системи сил відносно точки О 1  .
. (5.23)
(5.23) (5.24)
(5.24) Н відносно точки О початку системи координат хОу (рис. 5.25, б). Точка прикладання сили має координати А (хА =8 м, уА =10 м), а лінія її дії складає з віссю Ох кут
Н відносно точки О початку системи координат хОу (рис. 5.25, б). Точка прикладання сили має координати А (хА =8 м, уА =10 м), а лінія її дії складає з віссю Ох кут  .
.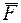 на координатні складові
на координатні складові  і
і  . Визначимо їх величини:
. Визначимо їх величини:  Н,
Н,  Н. За побудовою сила
Н. За побудовою сила 
 Н×м.
Н×м.
 б
Рис. 5.25
б
Рис. 5.25
 відносно полюса за загальною формулою
відносно полюса за загальною формулою  дуже складно, тому що невідомим є її плече h відносно точки О. Для його визначення спочатку необхідно скласти рівняння (5.23) або (5.24) лінії дії сили. Потім рівняння перпендикуляра з точки О на цю пряму, і далі визначити його довжину, яка і являтиме собою плече h сили
дуже складно, тому що невідомим є її плече h відносно точки О. Для його визначення спочатку необхідно скласти рівняння (5.23) або (5.24) лінії дії сили. Потім рівняння перпендикуляра з точки О на цю пряму, і далі визначити його довжину, яка і являтиме собою плече h сили 


