Відповідно до аксіоми 2 статики (див. розд. 1) прикладену до тіла силу можна переносити вздовж її лінії дії в будь-яку іншу його точку. При цьому дія сили на тіло, а також стан тіла не змінюються.
У ряді практичних задач рівноваги, пов’язаних зі спрощенням заданої системи сил, часто виникає необхідність перенесення сили до заданого центра паралельно самій до себе.
На відміну від попереднього випадку паралельне перенесення сили призводить в умовах збереження початкового механічного стану тіла до зміни системи діючих на нього силових факторів: до тіла необхідно додатково додати пару сил, параметри якої визначає наступна лема.
Лема. Прикладену до тіла в точці О (рис. 5.1,а) силу  можна перенести паралельно самій собі в будь-яку його іншу точку О 1 (центр приведення), додаючи при цьому, для збереження механічного стану тіла, пару сил
можна перенести паралельно самій собі в будь-яку його іншу точку О 1 (центр приведення), додаючи при цьому, для збереження механічного стану тіла, пару сил 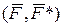 з моментом
з моментом 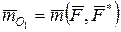 , рівним моменту
, рівним моменту 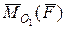 вихідної сили
вихідної сили  відносно центра приведення О 1.
відносно центра приведення О 1.
а б

в
Рис. 5.1
Доведення. Нехай у точці О (рис. 5.1,а) до тіла прикладена розташована в площині Е сила  . Позначимо систему сил, діючу на тіло, як (
. Позначимо систему сил, діючу на тіло, як ( ). Виберемо в тілі, в пл. Е, довільну точку О 1, положення якої визначимо вектором
). Виберемо в тілі, в пл. Е, довільну точку О 1, положення якої визначимо вектором 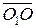 . Позначимо її як центр приведення “ О 1”. Прикладемо далі в пл. Е у цьому центрі (рис. 5.1,б) еквівалентну нулю систему
. Позначимо її як центр приведення “ О 1”. Прикладемо далі в пл. Е у цьому центрі (рис. 5.1,б) еквівалентну нулю систему 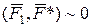 двох сил (двійку сил) з параметрами:
двох сил (двійку сил) з параметрами: 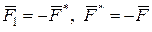 . При цьому, відповідно до аксіоми 2 статики, стан тіла не зміниться, а вихідна система сил (
. При цьому, відповідно до аксіоми 2 статики, стан тіла не зміниться, а вихідна система сил ( ) перетвориться в еквівалентну систему трьох сил:
) перетвориться в еквівалентну систему трьох сил: 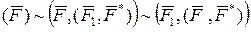 .
.
За побудовою на рис. 5.1,б, сила  прикладена в точці приведення О 1 і дорівнює
прикладена в точці приведення О 1 і дорівнює  , а система двох сил
, а система двох сил 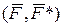 створює пару сил, що називається приєднаною парою сил. Далі в центрі приведення О 1 на рис. 5.1,в побудуємо вектор
створює пару сил, що називається приєднаною парою сил. Далі в центрі приведення О 1 на рис. 5.1,в побудуємо вектор 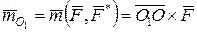 , рівний моменту отриманої пари сил, і вектор
, рівний моменту отриманої пари сил, і вектор 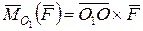 , рівний моменту вихідної сили
, рівний моменту вихідної сили  відносно полюса О 1. За визначенням вони є перпендикулярними до пл. Е, прикладеними в точці О 1 і рівними. Тобто момент приєднаної пари сил дорівнює моменту вихідної сили відносно нового центра приведення О 1:
відносно полюса О 1. За визначенням вони є перпендикулярними до пл. Е, прикладеними в точці О 1 і рівними. Тобто момент приєднаної пари сил дорівнює моменту вихідної сили відносно нового центра приведення О 1:
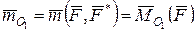 . (5.1)
. (5.1)
Отже лему доведено.
Рівняння (5.1) використовують на практиці при визначенні параметрів приєднаної пари сил 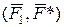 і сили
і сили  , які в більшості випадків являють собою прикладений до ланки механізму крутний момент і силу тиску ланки на вісь.
, які в більшості випадків являють собою прикладений до ланки механізму крутний момент і силу тиску ланки на вісь.

 Розглянемо, наприклад, барабан радіуса
Розглянемо, наприклад, барабан радіуса 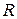 (рис. 5.2,а), до якого в точці А з боку намотаної нитки прикладено силу
(рис. 5.2,а), до якого в точці А з боку намотаної нитки прикладено силу  . Використуємо для сили
. Використуємо для сили  доведену лему, прийнявши за центр приведення точку О. У результаті отримаємо, що вихідна система сил (
доведену лему, прийнявши за центр приведення точку О. У результаті отримаємо, що вихідна система сил ( ) зводиться: до сили
) зводиться: до сили  (рівній
(рівній  ) і до пари сил
) і до пари сил 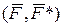 з моментом
з моментом 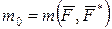 (рис. 5.2,а). При цьому на барабан діють: момент
(рис. 5.2,а). При цьому на барабан діють: момент 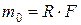 , який обертає барабан, і сила
, який обертає барабан, і сила  , що здійс-
, що здійс-
а б
Рис. 5.2
нює тиск на вісь барабану (рис. 5.2,б). Їх величини використовуються в подальшому при розв’язанні задач динаміки і міцності системи “опора - вісь - барабан - нитка”.

 можна перенести паралельно самій собі в будь-яку його іншу точку О 1 (центр приведення), додаючи при цьому, для збереження механічного стану тіла, пару сил
можна перенести паралельно самій собі в будь-яку його іншу точку О 1 (центр приведення), додаючи при цьому, для збереження механічного стану тіла, пару сил 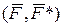 з моментом
з моментом 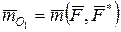 , рівним моменту
, рівним моменту 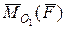 вихідної сили
вихідної сили 

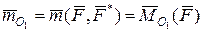

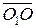 . Позначимо її як центр приведення “ О 1”. Прикладемо далі в пл. Е у цьому центрі (рис. 5.1,б) еквівалентну нулю систему
. Позначимо її як центр приведення “ О 1”. Прикладемо далі в пл. Е у цьому центрі (рис. 5.1,б) еквівалентну нулю систему 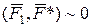 двох сил (двійку сил) з параметрами:
двох сил (двійку сил) з параметрами: 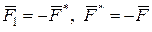 . При цьому, відповідно до аксіоми 2 статики, стан тіла не зміниться, а вихідна система сил (
. При цьому, відповідно до аксіоми 2 статики, стан тіла не зміниться, а вихідна система сил (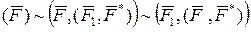 .
. прикладена в точці приведення О 1 і дорівнює
прикладена в точці приведення О 1 і дорівнює 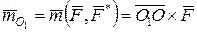 , рівний моменту отриманої пари сил, і вектор
, рівний моменту отриманої пари сил, і вектор 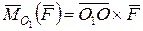 , рівний моменту вихідної сили
, рівний моменту вихідної сили 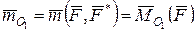 . (5.1)
. (5.1)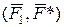 і сили
і сили 
 Розглянемо, наприклад, барабан радіуса
Розглянемо, наприклад, барабан радіуса 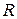 (рис. 5.2,а), до якого в точці А з боку намотаної нитки прикладено силу
(рис. 5.2,а), до якого в точці А з боку намотаної нитки прикладено силу 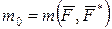 (рис. 5.2,а). При цьому на барабан діють: момент
(рис. 5.2,а). При цьому на барабан діють: момент 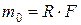 , який обертає барабан, і сила
, який обертає барабан, і сила