Відповідно до теореми Пуансо довільна система сил у просторі в загальному випадку зводиться у центрі О до двох силових факторів: сили, яка дорівнює головному вектору  , і пари сил з моментом, який дорівнює головному моменту
, і пари сил з моментом, який дорівнює головному моменту  вихідної системи сил. Однак, на практиці між параметрами (величинами і взаємним напрямком) векторів
вихідної системи сил. Однак, на практиці між параметрами (величинами і взаємним напрямком) векторів  і
і  виникають різні співвідношення, що призводять до окремих випадків приведення довільної системи сил.
виникають різні співвідношення, що призводять до окремих випадків приведення довільної системи сил.
5.4.1. Приведення системи сил до пари сил  з моментом
з моментом 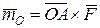 (рис. 5.8). У цьому випадку в центрі приведення О головний вектор системи
(рис. 5.8). У цьому випадку в центрі приведення О головний вектор системи  , а головний момент
, а головний момент  є перпендикулярним до пл. Е дії пари сил
є перпендикулярним до пл. Е дії пари сил  .
.
5.4.2. Приведення до рівнодійної  у центрі О. Тут (рис. 5.9) виконується наступне: головний момент системи сил
у центрі О. Тут (рис. 5.9) виконується наступне: головний момент системи сил  =0; головний вектор
=0; головний вектор  і належить пл. Е; система діючих на тіло сил відноситься до збіжної у точці О.
і належить пл. Е; система діючих на тіло сил відноситься до збіжної у точці О.

Рис. 5.8 Рис. 5.9

 5.4.3. Зрівноважена (нульова) система сил. У цьому випадку в центрі приведення О (рис. 5.10, 5.11) отримаємо: головний вектор
5.4.3. Зрівноважена (нульова) система сил. У цьому випадку в центрі приведення О (рис. 5.10, 5.11) отримаємо: головний вектор  і головний момент
і головний момент  ; вихідна система сил у будь-якій точці О тіла зводиться до еквівалентної нулю
; вихідна система сил у будь-якій точці О тіла зводиться до еквівалентної нулю  зрівноваженої системи; многокутники сил вихідної системи і многокутники векторів моментів сил відносно довільної точки О тіла є замкненими.
зрівноваженої системи; многокутники сил вихідної системи і многокутники векторів моментів сил відносно довільної точки О тіла є замкненими.
Рис. 5.10 Рис. 5.11
5.4.4. Приведення системи сил до головного вектора  і головного моменту
і головного моменту  , коли
, коли  . Тут мають місце, залежно від взаємної орієнтації векторів
. Тут мають місце, залежно від взаємної орієнтації векторів  і
і  , три окремі випадки.
, три окремі випадки.
 5.4.4.1. Приведення до динами, коли вектори
5.4.4.1. Приведення до динами, коли вектори  і
і  не є перпендикулярними, тобто (рис. 5.4) кут
не є перпендикулярними, тобто (рис. 5.4) кут  і скалярний добуток векторів
і скалярний добуток векторів  .
.
Розкладемо головний момент  на дві ортогональні складові
на дві ортогональні складові  , одна з яких спрямована вздовж головного вектора
, одна з яких спрямована вздовж головного вектора  .
.

Рис. 5.12 Рис. 5.13

Рис. 5.14 Рис. 5.15
Представимо момент 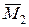 (закреслено на рис. 5.13) у вигляді пари сил
(закреслено на рис. 5.13) у вигляді пари сил  , в якій плече
, в якій плече  , а сила
, а сила  прикладена в точці О 1.
прикладена в точці О 1.
У цьому випадку буде виконуватись умова еквівалентності:  , тому що сили
, тому що сили  і
і  за визначенням складають двійку сил, тобто
за визначенням складають двійку сил, тобто  .
.
Представимо далі вектор 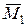 у вигляді моменту пари сил і перенесемо його, як вільний вектор, з точки О в точку О 1 прикладання сили
у вигляді моменту пари сил і перенесемо його, як вільний вектор, з точки О в точку О 1 прикладання сили  (показано на рис. 5.14 штриховою стрілкою).
(показано на рис. 5.14 штриховою стрілкою).
У результаті початкова система сил перетворилась в центрі О 1 в систему силових факторів 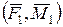 . Тут сила
. Тут сила  дорівнює головному вектору
дорівнює головному вектору  за визначенням, а момент
за визначенням, а момент 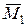 пари сил за величиною - проекції головного моменту
пари сил за величиною - проекції головного моменту  на напрямок головного вектора
на напрямок головного вектора  (рис. 5.12) системи сил:
(рис. 5.12) системи сил:  . На рис. 5.15 момент
. На рис. 5.15 момент 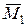 для наочності показано одночасно у вигляді пари сил
для наочності показано одночасно у вигляді пари сил  .
.
Сукупність діючих на тіло силових факторів у вигляді сили  і пари сил
і пари сил 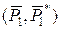 , вектори яких колінеарні (лежать на одній прямій), називають динамою чи динамічним гвинтом. Лінія, яка проходить через центр приведення О 1 вздовж даної прямої, називається віссю динами.
, вектори яких колінеарні (лежать на одній прямій), називають динамою чи динамічним гвинтом. Лінія, яка проходить через центр приведення О 1 вздовж даної прямої, називається віссю динами.
У просторі рівняння осі динами отримаємо з урахуванням умови паралельності векторів  і
і 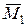 (рис. 5.14):
(рис. 5.14):
 (5.18)
(5.18)
де векторний добуток  , r - параметр гвинта (скаляр);
, r - параметр гвинта (скаляр);
 .
.
Враховуючи (5.18), отримаємо такі співвідношення між координатними складовими векторів  ,
,  і
і 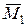 :
:
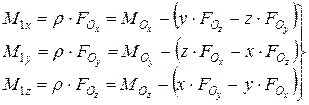 , (5.19)
, (5.19)
де х, у, z - координати точки О 1 на осі динами.
Співвідношення (5.19) дозволяють отримати рівняння прямої лінії, осі динами, у формі
 (5.20)
(5.20)
Отже, існує пряма з канонічним рівнянням (5.20) у проекціях, в будь-якій точці якої система діючих на тіло сил  зводиться до динами.
зводиться до динами.
Таким чином встановлено, що прикладена до тіла вихідна довільна система сил, якщо другий статичний інваріант першої форми не дорівнює нулю, тобто при  (
( ), зводиться у точці О 1 до динами, яка є сукупністю двох силових факторів: сили
), зводиться у точці О 1 до динами, яка є сукупністю двох силових факторів: сили  і моменту пари сил
і моменту пари сил 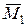 , вектори яких колінеарні. При цьому здається, що за величиною момент
, вектори яких колінеарні. При цьому здається, що за величиною момент  пари динами у точці О 1 буде найменшим (рис. 5.16), порівняно з моментами
пари динами у точці О 1 буде найменшим (рис. 5.16), порівняно з моментами  у будь-яких інших точках приведення Ок на осі Оу, тобто буде виконуватися співвідношення
у будь-яких інших точках приведення Ок на осі Оу, тобто буде виконуватися співвідношення  .
.
Цю важливу властивість динами використовують на практиці при вирішенні задач зрівноваження твердого тіла, а також відтворенні динамою заданого його руху за допомогою зовнішніх сил найменшої потужності.

Рис. 5.16
 5.4.4.2. Приведення до схрещеної системи двох сил. Цей випадок має місце, коли вихідна система сил
5.4.4.2. Приведення до схрещеної системи двох сил. Цей випадок має місце, коли вихідна система сил  приводиться у центрі О до головного вектора
приводиться у центрі О до головного вектора  і головного моменту
і головного моменту  (рис. 5.17), а кут
(рис. 5.17), а кут 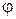 між векторами, як і у випадку приведення до динами, задовольняє співвідношенню
між векторами, як і у випадку приведення до динами, задовольняє співвідношенню  .
.
Представимо момент  (закреслено на рис. 5.17) у вигляді пари сил
(закреслено на рис. 5.17) у вигляді пари сил  з площиною дії Е і плечем
з площиною дії Е і плечем  (за величиною сила
(за величиною сила  пари може бути будь-якою). Далі додамо за правилом паралелограма вектори
пари може бути будь-якою). Далі додамо за правилом паралелограма вектори  і
і  , отримавши силу
, отримавши силу  .
.
Виконані перетворення призводять до наступної, еквівалентної до вихідної системи двох сил  і
і  :
:  .
.

Рис. 5.17
При цьому сила  є прикладеною у центрі приведення О, а точкою прикладання сили
є прикладеною у центрі приведення О, а точкою прикладання сили  є точка О 1 кінця плеча h пари сил
є точка О 1 кінця плеча h пари сил  . Важливою властивістю сили
. Важливою властивістю сили  є, однак, те, що вона не належить площині Е дії пари сил
є, однак, те, що вона не належить площині Е дії пари сил  .
.
Така сукупність діючих на тіло двох сил складає систему сил, щоі схрещуються (не лежать в одній площині) і не мають рівнодійної.
На відміну від динами отримана система силових факторів включає лише дві сили  ,
,  , тобто тут відсутня пара сил.
, тобто тут відсутня пара сил.
5.4.4.3. Приведення до однієї сили (рівнодійної), коли вектори  і
і  є перпендикулярними, тобто
є перпендикулярними, тобто  (рис. 5.18). У цьому випадку головний вектор
(рис. 5.18). У цьому випадку головний вектор  , лежить у площині Е, яка перпендикулярна головному моменту
, лежить у площині Е, яка перпендикулярна головному моменту  системи, тобто в площині дії результуючої приєднаної пари сил.
системи, тобто в площині дії результуючої приєднаної пари сил.
Представимо момент  (закреслено на рис. 5.18) у вигляді пари сил
(закреслено на рис. 5.18) у вигляді пари сил  з плечем
з плечем  і силою
і силою  .
.

Рис. 5.18
У результаті отримаємо, що сили  і
і  складають двійку сил, тобто систему сил
складають двійку сил, тобто систему сил  , а вихідна система виявляється еквівалентною одній силі
, а вихідна система виявляється еквівалентною одній силі  , яка належить площині Е, прикладена у точці О 1, що знаходиться на відстані
, яка належить площині Е, прикладена у точці О 1, що знаходиться на відстані  від початкового центра приведення О. Проведені еквівалентні перетворення мають наступний вигляд:
від початкового центра приведення О. Проведені еквівалентні перетворення мають наступний вигляд:
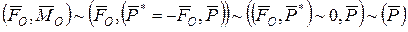 .
.
Вони зводять вихідну систему сил  до однієї сили
до однієї сили  (рівнодійної), яка дорівнює головному вектору
(рівнодійної), яка дорівнює головному вектору  системи і прикладена у новому центрі приведення О 1.
системи і прикладена у новому центрі приведення О 1.

 , і пари сил з моментом, який дорівнює головному моменту
, і пари сил з моментом, який дорівнює головному моменту  вихідної системи сил. Однак, на практиці між параметрами (величинами і взаємним напрямком) векторів
вихідної системи сил. Однак, на практиці між параметрами (величинами і взаємним напрямком) векторів  з моментом
з моментом 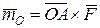 (рис. 5.8). У цьому випадку в центрі приведення О головний вектор системи
(рис. 5.8). У цьому випадку в центрі приведення О головний вектор системи  , а головний момент
, а головний момент  є перпендикулярним до пл. Е дії пари сил
є перпендикулярним до пл. Е дії пари сил  у центрі О. Тут (рис. 5.9) виконується наступне: головний момент системи сил
у центрі О. Тут (рис. 5.9) виконується наступне: головний момент системи сил  і належить пл. Е; система діючих на тіло сил відноситься до збіжної у точці О.
і належить пл. Е; система діючих на тіло сил відноситься до збіжної у точці О.

 5.4.3. Зрівноважена (нульова) система сил. У цьому випадку в центрі приведення О (рис. 5.10, 5.11) отримаємо: головний вектор
5.4.3. Зрівноважена (нульова) система сил. У цьому випадку в центрі приведення О (рис. 5.10, 5.11) отримаємо: головний вектор  і головний момент
і головний момент  ; вихідна система сил у будь-якій точці О тіла зводиться до еквівалентної нулю
; вихідна система сил у будь-якій точці О тіла зводиться до еквівалентної нулю  зрівноваженої системи; многокутники сил вихідної системи і многокутники векторів моментів сил відносно довільної точки О тіла є замкненими.
зрівноваженої системи; многокутники сил вихідної системи і многокутники векторів моментів сил відносно довільної точки О тіла є замкненими. і головного моменту
і головного моменту  , коли
, коли  . Тут мають місце, залежно від взаємної орієнтації векторів
. Тут мають місце, залежно від взаємної орієнтації векторів  5.4.4.1. Приведення до динами, коли вектори
5.4.4.1. Приведення до динами, коли вектори  і скалярний добуток векторів
і скалярний добуток векторів  .
. , одна з яких спрямована вздовж головного вектора
, одна з яких спрямована вздовж головного вектора 

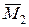 (закреслено на рис. 5.13) у вигляді пари сил
(закреслено на рис. 5.13) у вигляді пари сил  , в якій плече
, в якій плече  , а сила
, а сила  прикладена в точці О 1.
прикладена в точці О 1. , тому що сили
, тому що сили  і
і  за визначенням складають двійку сил, тобто
за визначенням складають двійку сил, тобто  .
.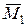 у вигляді моменту пари сил і перенесемо його, як вільний вектор, з точки О в точку О 1 прикладання сили
у вигляді моменту пари сил і перенесемо його, як вільний вектор, з точки О в точку О 1 прикладання сили  (показано на рис. 5.14 штриховою стрілкою).
(показано на рис. 5.14 штриховою стрілкою).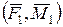 . Тут сила
. Тут сила  на напрямок головного вектора
на напрямок головного вектора  . На рис. 5.15 момент
. На рис. 5.15 момент  .
.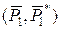 , вектори яких колінеарні (лежать на одній прямій), називають динамою чи динамічним гвинтом. Лінія, яка проходить через центр приведення О 1 вздовж даної прямої, називається віссю динами.
, вектори яких колінеарні (лежать на одній прямій), називають динамою чи динамічним гвинтом. Лінія, яка проходить через центр приведення О 1 вздовж даної прямої, називається віссю динами. (5.18)
(5.18) , r - параметр гвинта (скаляр);
, r - параметр гвинта (скаляр); .
.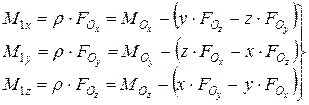 , (5.19)
, (5.19) (5.20)
(5.20) зводиться до динами.
зводиться до динами. (
( ), зводиться у точці О 1 до динами, яка є сукупністю двох силових факторів: сили
), зводиться у точці О 1 до динами, яка є сукупністю двох силових факторів: сили  пари динами у точці О 1 буде найменшим (рис. 5.16), порівняно з моментами
пари динами у точці О 1 буде найменшим (рис. 5.16), порівняно з моментами  у будь-яких інших точках приведення Ок на осі Оу, тобто буде виконуватися співвідношення
у будь-яких інших точках приведення Ок на осі Оу, тобто буде виконуватися співвідношення  .
.
 5.4.4.2. Приведення до схрещеної системи двох сил. Цей випадок має місце, коли вихідна система сил
5.4.4.2. Приведення до схрещеної системи двох сил. Цей випадок має місце, коли вихідна система сил  приводиться у центрі О до головного вектора
приводиться у центрі О до головного вектора 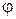 між векторами, як і у випадку приведення до динами, задовольняє співвідношенню
між векторами, як і у випадку приведення до динами, задовольняє співвідношенню  .
. з площиною дії Е і плечем
з площиною дії Е і плечем  (за величиною сила
(за величиною сила  пари може бути будь-якою). Далі додамо за правилом паралелограма вектори
пари може бути будь-якою). Далі додамо за правилом паралелограма вектори  , отримавши силу
, отримавши силу  .
. і
і  .
.
 (рис. 5.18). У цьому випадку головний вектор
(рис. 5.18). У цьому випадку головний вектор  і силою
і силою  .
.
 , а вихідна система виявляється еквівалентною одній силі
, а вихідна система виявляється еквівалентною одній силі 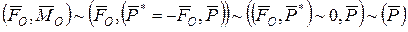 .
. до однієї сили
до однієї сили 


