Теорема про три непаралельні сили ⇐ Предыдущая3456789101112Следующая ⇒   Теорему про рівновагу трьох непаралельних сил застосовують в тих випадках, коли треба знайти дві невідомі сили (реакції в’язів), які зрівноважують третю відому силу (наприклад, силу ваги тіла), якщо відомо точку прикладання однієї з невідомих сил і лінію дії іншої. Теорема. Якщо тіло перебуває в рівновазі під дією трьох непаралельних сил, з яких принаймні дві лежать в одній площині, то лінії дії всіх трьох сил перетинаються в одній точці, а вектори сил утворюють замкнений трикутник. С Рис. 3.3

Доведення. Нехай тіло перебуває в рівновазі під дією трьох непаралельних сил з яких і лежать в одній площині (рис. 3.3). Продовжимо лінії дії сил , і знайдемо їх точку перетину О. Перенесемо сили і вздовж їх ліній дії в точку О і знайдемо

їх рівнодійну 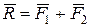. Замінивши сили і їх рівнодійною ,

одержимо, що дане тіло перебуває в рівновазі під дією тільки двох сил і .

Це можливо, враховуючи аксіому 1 про дві сили, тільки якщо сили і мають спільну лінію дії, тобто коли лінія дії сили проходить через точку О. Теорему доведено.

Зауважимо, що доведена теорема визначає необхідну, але не достатню умову рівноваги тіла під дією трьох сил. Дійсно, тіло під дією трьох сил, лінії дії яких перетинаються в одній точці, може і не перебувати в рівновазі, а здійснювати поступальний рівномірний рух, відповідно до першого закону Ньютона.

Застосувавши до заданої системи трьох сил геометричну умову рівноваги, дістаємо також, що трикутник сил буде замкнений: кінець третьої сили буде збігатися з початком першої сили .

Приклад. Розглянемо, наприклад, зображену на рис. 3.4,а механічну схему, що складається з бруса вагою Р, який спирається кінцем на прямокутний виступ Д і закріплений в точці А з підлогою через нерухому шарнірну опору. Визначимо реакції опор, якщо .

 

 

б

 

 

а Рис. 3.4

Розв’язання. Лінії дії сили ваги і реакції в’язі у точці D відомі. Через точку О їх перетину, відповідно до теореми про три сили, повинна проходити невідома лінія дії реакції . Будуємо її на схемі. З урахуванням визначених ліній дій реакції , і відомої сили будуємо замкнений силовий трикутник (рис. 3.4,б) , який подібний трикутнику на рис. 3.4,а. Силовий трикутник дозволяє визначити не тільки напрями реакцій , , але і їх величини. Для цього треба використати умови пропорційності сторін подібних трикутників , а також теорему косинусів .