Приведення до рівнодійної. Правило многокутника сил
Найпростішою є система збіжних сил, тобто система сил, лінії дії яких перетинаються в одній точці (точці О збігу сил). Вона може бути просторовою чи плоскою. В останньому випадку всі лінії дії сил системи належать одній площині. Теорема про рівновагу. Система збіжних сил Доведення. Розглянемо (рис. 3.1,а) вихідну систему збіжних сил Для кожної сили системи використовуємо аксіому 2 про перенесення сили уздовж лінії дії в точку О збігу (рис. 3.1,б). У результаті отримаємо систему сил На основі аксіоми 3 про паралелограм сил будь-яку кількість сил із загальною точкою прикладання можна складати геометрично. При цьому можна використовувати або правило паралелограма, або правило трикутника (многокутника). У першому випадку (рис. 3.1,б), застосовуючи послідовно правило паралелограма, дістанемо спочатку рівнодійну За правилом многокутника рівнодійну сил (рис. 3.1,в) визначаємо як суму векторів цих сил: для цього з кінця вектора
в) б) Рис. 3.1
Одержаний таким чином многокутник має назву многокутника сил, або силового многокутника, замикальна сторона якого виявляється рівнодійною силою системи. Таким чином, теорему доведено. Доведена теорема дозволяє розв’язувати задачу приведення систем збіжних сил до рівнодійної сили графічно (нею зручно користуватись у разі плоскої довільної системи сил). Рівнодійну
де Величина (модуль) і напрямні косинуси рівнодійної сили
Визначивши проекції або величину і напрямні косинуси рівнодійної, можна побудувати і сам вектор
а б Рис. 3.2
додавання векторів початкових сил за правилом паралелограма, а також методом додавання координатних складових рівнодійної за правилом прямокутника (плоска система сил) або паралелепіпеда (просторова система) чи за правилом “модуль-кут”. У першому випадку будуємо на силах
У другому випадку отримаємо: проекції рівнодійної
координатні складові рівнодійної:
Вектори За правилом “модуль-кут” визначаємо величину рівнодійної
|

 еквівалентна одній силі (рівнодійній
еквівалентна одній силі (рівнодійній  ), яка дорівнює геометричній (векторній) сумі цих сил
), яка дорівнює геометричній (векторній) сумі цих сил  і прикладена в точці О їх збігу.
і прикладена в точці О їх збігу. і точками прикладання
і точками прикладання  .
. , далі отримаємо рівнодійну
, далі отримаємо рівнодійну 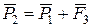 і нарешті рівнодійну
і нарешті рівнодійну  заданої системи сил (рис. 3.1,б).
заданої системи сил (рис. 3.1,б). відкладаємо вектор сили
відкладаємо вектор сили  , і т.д. З’єднавши початок першого вектора
, і т.д. З’єднавши початок першого вектора  , визначимо рівнодійну силу
, визначимо рівнодійну силу
 а)
а)
 .
. на осі прямокутної системи координат методами векторної алгебри. У даному випадку рівнодійну
на осі прямокутної системи координат методами векторної алгебри. У даному випадку рівнодійну  , (3.1)
, (3.1) ;
;  ;
;  ;
;  - проекції сил системи на відповідні осі координат;
- проекції сил системи на відповідні осі координат;  - координатні складові рівнодійної.
- координатні складові рівнодійної.


 ; (3.2)
; (3.2)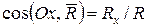 ;
;  ;
;  .
. Розглянемо, наприклад, задану в площині хОу (рис. 3.2,а) систему двох збіжних сил
Розглянемо, наприклад, задану в площині хОу (рис. 3.2,а) систему двох збіжних сил  Н,
Н,  Н. Визначимо рівнодійну
Н. Визначимо рівнодійну  , як на сторонах, паралелограм (рис. 3.2,а), діагональ якого буде шуканою рівнодійною
, як на сторонах, паралелограм (рис. 3.2,а), діагональ якого буде шуканою рівнодійною  (Н).
(Н). (Н),
(Н), (Н),
(Н),
 .
. і
і  будуємо на рис. 3.2,б. Склавши їх за правилом прямокутника, отримаємо шукану рівнодійну
будуємо на рис. 3.2,б. Склавши їх за правилом прямокутника, отримаємо шукану рівнодійну  (Н), її напрямний косинус
(Н), її напрямний косинус і кут
і кут  . Будуємо в площині хОу лінію дії а-а рівнодійної (рис. 3.2,б), враховуючи визначений кут між нею і віссю Ох. Далі на лінії дії а-а будуємо вектор рівнодійної, який починається в полюсі О системи координат і має величину (довжину)
. Будуємо в площині хОу лінію дії а-а рівнодійної (рис. 3.2,б), враховуючи визначений кут між нею і віссю Ох. Далі на лінії дії а-а будуємо вектор рівнодійної, який починається в полюсі О системи координат і має величину (довжину)  (Н).
(Н).


