Елементи прямокутного профілю
При проектуванні елементів прямокутного профілю, що згинаються, можуть виникати різні задачі підбору поздовжньої арматури. Найчастіше зустрічаються задачі підбору нижньої розтягнутої арматури при умовній чи фактичній відсутності верхньої (стиснутої) арматури. Такі задачі називаються – підбір арматури в згинаних елементах з одиночною арматурою.
Умову міцності для таких елементів записують у вигляді

| (3.4)
| або  . .
| (3.5)
| Висоту стиснутої зони визначають з рівняння
| RsAs = Rb × b × x;
| (3.6)
|  . .
| (3.7)
| Для підбору арматури користуються табличним способом. Сутність його полягає в наступному. При заданому зовнішньому моменті М и параметрах перерізу b і h визначають коефіцієнт 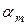 : :
 . .
| (3.8)
| За цим коефіцієнтом з табл.3.1 визначають допоміжні коефіцієнти  і z. Значення і z. Значення 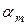 , ξ і z можна інтерполювати. У деяких літературних джерелах параметри , ξ і z можна інтерполювати. У деяких літературних джерелах параметри 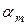 , z і , z і  позначені позначені  , , 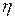 і і  . .
За параметром ξ; перевіряють умову ξ £ ξR, а потім знаходять розрахункову площу арматури:
 . .
| (3.9)
| Користуючись сортаментом арматури (додаток III), підбирають конкретну площу арматури з вказівкою її діаметра. Після чого перевіряють відсоток армування перерізу
 . .
| (3.10)
| Таблиця 3.1 – Допоміжна таблиця для розрахунку
елементів прямокутного перерізу, що згинаються, з одиночною арматурою
| ξ = x/h0
| z= 1– 0,5 ξ;
| 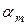
| ξ = x/h0
| z= 1– 0,5 ξ;
| 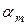
| | 0,01
| 0,995
| 0,01
| 0,36
| 0,82
| 0,295
| | 0,02
| 0,99
| 0,02
| 0,37
| 0,815
| 0,301
| | 0,03
| 0,985
| 0,03
| 0,38
| 0,81
| 0,309
| | 0,04
| 0,98
| 0,039
| 0,39
| 0,805
| 0,314
| | 0,05
| 0,975
| 0,048
| 0,4
| 0,8
| 0,32
| | 0,06
| 0,97
| 0,058
| 0,41
| 0,795
| 0,326
| | 0,07
| 0,965
| 0,067
| 0,42
| 0,79
| 0,332
| | 0,08
| 0,96
| 0,077
| 0,43
| 0,785
| 0,337
| | 0,09
| 0,955
| 0,085
| 0,44
| 0,78
| 0,343
| | 0,10
| 0,95
| 0,095
| 0,45
| 0,775
| 0,349
| | 0,11
| 0,945
| 0,104
| 0,46
| 0,77
| 0,354
| | 0,12
| 6,94
| 0,113
| 0,47
| 0,765
| 0,359
| | 0,13
| 0,935
| 0,121
| 0,48
| 0,76
| 0,365
| | 0,14
| 0,93
| 0,13
| 0,49
| 0,755
| 0,37
| | 0,15
| 0,925
| 0,139
| 0,5
| 0,75
| 0,375
| | 0,16
| 0,92
| 0,147
| 0,51
| 0,745
| 0,38
| | 0,17
| 0,915
| 0,165
| 0,52
| 0,74
| 0,385
| | 0,18
| 0,91
| 0,164
| 0,53
| 0,735
| 0,39
| | 0,19
| 0,905
| 0,172
| 0,54
| 0,73
| 0,394
| | 0,2
| 0,9
| 0,18
| 0,55
| 0,725
| 0,399
| | 0,21
| 0,895
| 0,188
| 0,56
| 0,72
| 0,403
| | 0,22
| 0,89
| 0,196
| 0,57
| 0,715
| 0,408
| | 0,23
| 0,885
| 0,203
| 0,58
| 0,71
| 0,412
| | 0,24
| 0,88
| 0,211
| 0,59
| 0,705
| 0,416
| | 0,25
| 0,875
| 0,219
| 0,6
| 0,7
| 0,42
| | 0,26
| 0,87
| 0,226
| 0,61
| 0,695
| 0,424
| | 0,27
| 0,865
| 0,236
| 0,62
| 0,69
| 0,428
| | 0,28
| 0,86
| 0,241
| 0,63
| 0,685
| 0,432
| | 0,29
| 0,855
| 0,248
| 0,64
| 0,68
| 0,435
| | 0,3
| 0,85
| 0,255
| 0,65
| 0,675
| 0,439
| | 0,31
| 0,845
| 0,262
| 0,66
| 0,67
| 0,442
| | 0,32
| 0,84
| 0,269
| 0,67
| 0,665
| 0,446
| | 0,33
| 0,835
| 0,275
| 0,68
| 0,66
| 0,449
| | 0,34
| 0,83
| 0,282
| 0,69
| 0,655
| 0,452
| | 0,35
| 0,825
| 0,289
| 0,7
| 0,65
| 0,455
| Якщо елемент, що згинається, має подвійну арматуру, тоді можливі дві проектно-розрахункові задачі:
1. Задано розміри b і h і зовнішній момент М. Потрібно визначити площі перерізів As і A's.
Приймається рівність 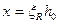 , тоді можна визначити А's, користуючись рівнянням (3.2): , тоді можна визначити А's, користуючись рівнянням (3.2):
 ; ;  , ,
| (3.11)
| а потім з рівняння (3.1) визначається As:
 . .
| (3.12)
| 2. Задано розміри b і h і стиснута арматура A's, а також зовнішній момент М. Потрібно визначити As.
Спочатку визначається параметр 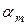 : :
 ; ;
| (3.13)
| Потім з табл.3.1 знаходять значення ξ;, після чого знаходять As:
 ; ;
| (3.14)
| Якщо виявиться, що 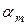 > >  = 0,455, тоді площу A's збільшують до таких значень = 0,455, тоді площу A's збільшують до таких значень 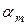 , щоб воно стало менше , щоб воно стало менше  , або збільшують розміри перерізу , або збільшують розміри перерізу 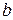 і і 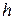 . .
Приклад 1. Прямокутний переріз має розміри 200х400 мм (рис.3.4). Зовнішній момент М = 120 кН×м, бетон В25 (Rb = 14,5 МПа). Робоча одиночна арматура класу А-III (400С), Rs = 365 МПа.
Визначаємо параметр 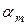 за формулою (3.8); z і ξ; знаходимо за табл.3.1: за формулою (3.8); z і ξ; знаходимо за табл.3.1:
 ; z = 0,815; ξ; = 0,37. ; z = 0,815; ξ; = 0,37.
Знаходимо розрахункову площу арматури, користуючись формулою (3.9):
 см2. см2.
За сортаментом підбираємо 2Æ18 + 2Æ20 із загальною площею As = 11,37 см2.

| | Рис. 3.4
| При обчисленні значень 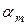 і і  необхідно строго стежити, щоб розмірність усіх величин, що підставляються у формули (3.8) і (3.9), була в однакових одиницях, тобто в кН×м чи кН×см. Додатково треба перевірити умову ξ; £ ξR, користуючись формулою (3.3). необхідно строго стежити, щоб розмірність усіх величин, що підставляються у формули (3.8) і (3.9), була в однакових одиницях, тобто в кН×м чи кН×см. Додатково треба перевірити умову ξ; £ ξR, користуючись формулою (3.3).

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|

Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах...
|
Понятие метода в психологии. Классификация методов психологии и их характеристика Метод – это путь, способ познания, посредством которого познается предмет науки (С...
ЛЕКАРСТВЕННЫЕ ФОРМЫ ДЛЯ ИНЪЕКЦИЙ К лекарственным формам для инъекций относятся водные, спиртовые и масляные растворы, суспензии, эмульсии, новогаленовые препараты, жидкие органопрепараты и жидкие экстракты, а также порошки и таблетки для имплантации...
Тема 5. Организационная структура управления гостиницей 1. Виды организационно – управленческих структур. 2. Организационно – управленческая структура современного ТГК...
|
Принципы, критерии и методы оценки и аттестации персонала
Аттестация персонала является одной их важнейших функций управления персоналом...
Пункты решения командира взвода на организацию боя. уяснение полученной задачи; оценка обстановки; принятие решения; проведение рекогносцировки; отдача боевого приказа; организация взаимодействия...
Что такое пропорции?
Это соотношение частей целого между собой. Что может являться частями в образе или в луке...
|
|


 .
.
 .
.
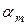 :
: .
.
 і z. Значення
і z. Значення  ,
, 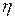 і
і  .
.
 .
.
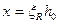 , тоді можна визначити А's, користуючись рівнянням (3.2):
, тоді можна визначити А's, користуючись рівнянням (3.2): ;
;  ,
,
 .
.
 ;
;
 ;
;
 = 0,455, тоді площу A's збільшують до таких значень
= 0,455, тоді площу A's збільшують до таких значень 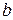 і
і 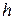 .
. ; z = 0,815; ξ; = 0,37.
; z = 0,815; ξ; = 0,37. см2.
см2.
 необхідно строго стежити, щоб розмірність усіх величин, що підставляються у формули (3.8) і (3.9), була в однакових одиницях, тобто в кН×м чи кН×см. Додатково треба перевірити умову ξ; £ ξR, користуючись формулою (3.3).
необхідно строго стежити, щоб розмірність усіх величин, що підставляються у формули (3.8) і (3.9), була в однакових одиницях, тобто в кН×м чи кН×см. Додатково треба перевірити умову ξ; £ ξR, користуючись формулою (3.3).


