Нехай у просторі задано деяку точку  (мал.1), зображення якої треба побудувати на площині
(мал.1), зображення якої треба побудувати на площині  і точку
і точку  . Яку назвемо центром проекцій. Точка
. Яку назвемо центром проекцій. Точка  не суміщається з точкою
не суміщається з точкою  .
.


Провівши через точку пряму до перетину з площиною, дістанемо точку, яка і є центральною проекцією заданої точки на площину.
Паралельне проектування визначається площиною  і напрямом
і напрямом  проектування на цю площину,
проектування на цю площину,  не паралельно
не паралельно  .
.
Приклад 3.
Нехай у просторі задано деяку точку  (мал. 2), зображення якої треба побудувати на площині
(мал. 2), зображення якої треба побудувати на площині  в заданому напрямі
в заданому напрямі  проектування.
проектування.
Провівши через точку  пряму, паралельну
пряму, паралельну  , до перетину з площиною
, до перетину з площиною  дістанемо точку
дістанемо точку 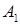 , яка і є паралельною проекцією заданої точки
, яка і є паралельною проекцією заданої точки  на площину
на площину  .
.
В обох випадках площину  називають площиною проекцій,
називають площиною проекцій,  або
або  (мал. 3) – проектуючи прямою або проектуючим променем, точку
(мал. 3) – проектуючи прямою або проектуючим променем, точку 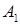 - центральною (паралельною) проекцією точки
- центральною (паралельною) проекцією точки  . Точку
. Точку  - називають оригіналом або проектуючою фігурою. Точка
- називають оригіналом або проектуючою фігурою. Точка 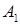 - єдина.
- єдина.
Означення. Пряма, що проходить через центр проекцій  ( при центральному проектуванні)або паралельна напряму проектування
( при центральному проектуванні)або паралельна напряму проектування  (при паралельному проектуванні), називається проектуючою прямою.
(при паралельному проектуванні), називається проектуючою прямою.
Означення. Проекцією 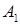 будь-якої точки
будь-якої точки  називають точку перетину проектуючої прямої
називають точку перетину проектуючої прямої  з площиною проекцій
з площиною проекцій  .
.
Те що точка є проекцією точки на площину, скорочено записуємо так:. Якщо точка-оригінал, наприклад, суміщається зі своєю проекцією, на площину проекцій, то записують:.

 (мал.1), зображення якої треба побудувати на площині
(мал.1), зображення якої треба побудувати на площині  і точку
і точку  . Яку назвемо центром проекцій. Точка
. Яку назвемо центром проекцій. Точка 

 проектування на цю площину,
проектування на цю площину, 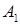 , яка і є паралельною проекцією заданої точки
, яка і є паралельною проекцією заданої точки  або
або  (мал. 3) – проектуючи прямою або проектуючим променем, точку
(мал. 3) – проектуючи прямою або проектуючим променем, точку 


