Через точку проведемо пряму , паралельну прямій , і пряму паралельну прямій . Задавши на прямій ( ) яку-небудь точку закінчуємо розв‘язання задачі на побудову (мал. 13).
Увага учнів звертається на те, що в першому розв‘язанні ні побудова площини Ще слід звернути увагу учнів на те, що не визначає рішення виконане ілюстративне креслення, так як на ньому пряма Далі як розв‘язання так і аналіз наступних задач вони можуть виконати самостійно. 1 ). Через точку, яка розташована поза даною площиною, провести пряму, паралельну даній площині. 2). Через пряму, паралельну даній площині, провести площину, паралельну даній. 3). Через точку, яка не належить двом мимобіжнимпрямим, провести площину, паралельну цим прямим. При дотриманні «методичних мір» у навчанні розв‘язанню задач на уявлювану побудову їх кількість можна збільшити у порівнянні з кількістю задач, які рекомендовані для розв‘язання програмами. 4). Через дану пряму провести площину, паралельну іншій даній прямій. 5). Через дану точку в просторі провести площину, перпендикулярну даній прямій. 6). Через дану точку провести пряму, перпендикулярну даній площині. 7). Через дану точку провести площину, перпендикулярну даній площині і паралельну даній прямій.
|
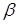, ні побудова прямої 
фактично не виконувалося, що в наведених операціях признається тільки факт існування площини 
служить зображенням не тільки прямої, параллельної прямій 
.
