Дано куб 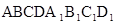 і точки
і точки  ,
,  і
і  такі, що
такі, що 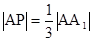 ,
, 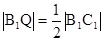 , а точка
, а точка  - центроїд грані
- центроїд грані 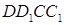 . Побудувати переріз куба площиною
. Побудувати переріз куба площиною 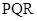 .
.
Розв‘язання.
Як і в попередньому прикладі, знаходимо точки 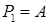 ,
, 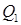 і
і 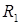 . Аналогічно попередньому прикладу знаходимо слід січної площини (мал. 29), отримаємо шуканий переріз.
. Аналогічно попередньому прикладу знаходимо слід січної площини (мал. 29), отримаємо шуканий переріз.
Побудову перерізу циліндра і конуса виконуємо за аналогією до побудови перерізу призми і піраміди площиною. якщо уявити, що в циліндр (конус) вписано n-кутну призму (піраміду), то бічні ребра призми (піраміди) – є не що інше, як твірні циліндра (конуса). Отже, вершини шуканого перерізу будуть розміщені на твірних циліндра (конуса): це точки перетину січної площини  з твірними циліндра чи конуса.
з твірними циліндра чи конуса.
Щоб побудувати лінію перерізу циліндра (конуса) площиною, слід визначити точки перетину контурних прямих з даною площиною.
Приклад 12.
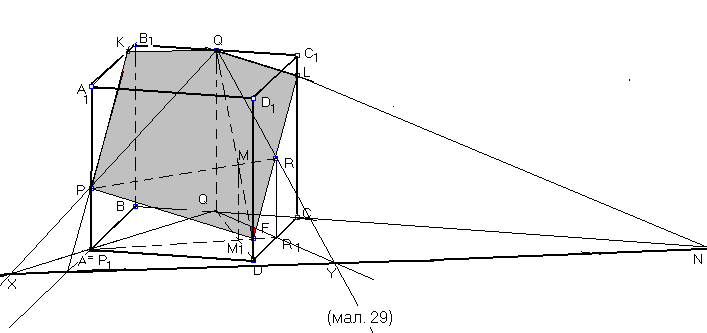
Побудувати переріз циліндра площиною, яка задана слідом а в нижній основі і точкою на видимій частині циліндричної поверхні.
Розв‘язання.
За умовою точка 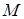 належить бічній поверхні циліндра, отже, вона належить і шуканій лінії перерізу. Щоб побудувати ще кілька точок, які визначають контур перерізу, міркуватимемо так. Січна площина перетинає контурні прямі
належить бічній поверхні циліндра, отже, вона належить і шуканій лінії перерізу. Щоб побудувати ще кілька точок, які визначають контур перерізу, міркуватимемо так. Січна площина перетинає контурні прямі 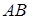 і
і 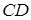 в деяких точках
в деяких точках 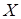 і
і 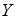 , ортогональні проекції яких на основній площині
, ортогональні проекції яких на основній площині 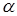 відомі
відомі 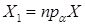 , якщо
, якщо  , то
, то 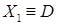 ,
, 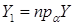 , якщо
, якщо 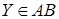 , то
, то 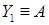 (мал. 30).
(мал. 30).
Пряма належить основній площині, тому. Знаючи проекцію прямої-оригіналу на пл. і одну точку цієї прямої, можна визначити другу її точку, яка належить і прямій а, по якій січна площина перетинає пл..
1. 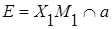 .
.
Через те що пряма 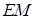 і відрізок
і відрізок 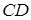 належать одній площині, і не паралельні між собою, то:
належать одній площині, і не паралельні між собою, то:
2. 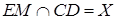 ,
,
3. 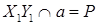 .
.
Через те що точки 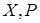 і твірна
і твірна 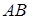 належать одній площині, то:
належать одній площині, то:
4. 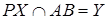 .
.
Коли січна площина перетинає всі твірні циліндра, то перерізом буде еліпс. Трьох точок 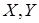 і
і 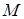 не достатньо для його побудови. Треба побудувати ще кілька точок, які належать еліпсу перерізу. Кожна з цих точок належить твірним циліндра, які. Проекції цих точок належать колу, що є основою циліндра і одночасно є основами твірних циліндра, які проходять через зазначені точки.
не достатньо для його побудови. Треба побудувати ще кілька точок, які належать еліпсу перерізу. Кожна з цих точок належить твірним циліндра, які. Проекції цих точок належать колу, що є основою циліндра і одночасно є основами твірних циліндра, які проходять через зазначені точки.
Вибравши довільно точки 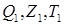 на основі циліндра, проводимо через них твірні, які “несуть” на собі точки-оригінали
на основі циліндра, проводимо через них твірні, які “несуть” на собі точки-оригінали 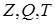 .
.
5. 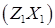 ,
,
6. 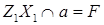 ,
,
7. 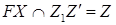 .
.
8. 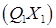 ,
,
9. 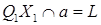 ,
,
10. 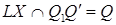 .
.
11. 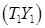 ,
,
12. 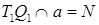 ,
,
13. 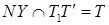 .
.
Побудовані точки 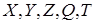 , як і задана точка
, як і задана точка 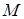 , належать поверхні циліндра, а тому і визначають лінію, по якій січна площина перетинає його. Сполучивши точки
, належать поверхні циліндра, а тому і визначають лінію, по якій січна площина перетинає його. Сполучивши точки 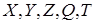 плавною кривою дістанемо наочне зображення фігури перерізу – еліпс.
плавною кривою дістанемо наочне зображення фігури перерізу – еліпс.

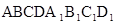 і точки
і точки  ,
,  і
і  такі, що
такі, що 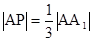 ,
, 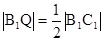 , а точка
, а точка 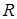 - центроїд грані
- центроїд грані 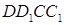 . Побудувати переріз куба площиною
. Побудувати переріз куба площиною 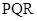 .
.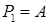 ,
, 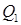 і
і 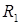 . Аналогічно попередньому прикладу знаходимо слід січної площини (мал. 29), отримаємо шуканий переріз.
. Аналогічно попередньому прикладу знаходимо слід січної площини (мал. 29), отримаємо шуканий переріз.
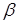 з твірними циліндра чи конуса.
з твірними циліндра чи конуса.
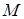 належить бічній поверхні циліндра, отже, вона належить і шуканій лінії перерізу. Щоб побудувати ще кілька точок, які визначають контур перерізу, міркуватимемо так. Січна площина перетинає контурні прямі
належить бічній поверхні циліндра, отже, вона належить і шуканій лінії перерізу. Щоб побудувати ще кілька точок, які визначають контур перерізу, міркуватимемо так. Січна площина перетинає контурні прямі 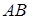 і
і 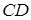 в деяких точках
в деяких точках 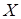 і
і 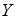 , ортогональні проекції яких на основній площині
, ортогональні проекції яких на основній площині 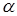 відомі
відомі 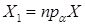 , якщо
, якщо  , то
, то 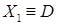 ,
, 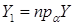 , якщо
, якщо 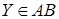 , то
, то 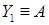 (мал. 30).
(мал. 30).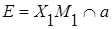 .
.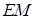 і відрізок
і відрізок 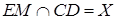 ,
,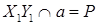 .
.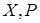 і твірна
і твірна 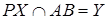 .
.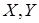 і
і 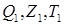 на основі циліндра, проводимо через них твірні, які “несуть” на собі точки-оригінали
на основі циліндра, проводимо через них твірні, які “несуть” на собі точки-оригінали 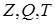 .
.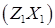 ,
,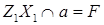 ,
,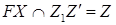 .
.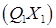 ,
,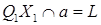 ,
,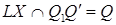 .
.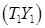 ,
,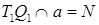 ,
,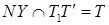 .
.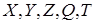 , як і задана точка
, як і задана точка 


