Приклад 1. Побудувати переріз піраміди, який проходить через точки , і .
Побудувати переріз піраміди, який проходить через точки 1 метод – метод сліду. Розв‘язання. Знайдемо проекції точок Знайдемо слід січної площини – лінію перетину площини 1) Так як 2) Точка 2) Далі: 3) 4) 5) Так як 6) 7) Оскільки за побудовою вершини чотирикутника Так як за змістом задачі точки 2 метод – метод внутрішнього проектування. Розв‘язання. Як і в попередньому прикладі знайдемо проекції точок 1) 2) 3) 4) Ясно, що 5) 6) 7) Отриманий чотирикутник
Засоби завдання перерізів многокутників дуже різноманітні. Січна площина може бути задана двома точками та якоюсь прямою, якою заданий переріз паралельно або перпендикулярно, двома точками і площиною, якою задано переріз паралельно або перпендикулярно, і т. д.
|

 ,
,  і
і  .
. :
:  ,
, 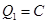 , точка
, точка  проектується в точку
проектується в точку 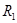 .
. з площиною
з площиною 
 , а
, а  , то
, то  . Так як
. Так як  , а
, а  , то
, то  . Таким чином точка
. Таким чином точка 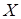 являється спільною точкою двох площин
являється спільною точкою двох площин  та
та  .
.
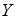 також являється спільною точкою двох площин. Тоді
також являється спільною точкою двох площин. Тоді  - пряма, по якій перетинаються площини
- пряма, по якій перетинаються площини  тобто
тобто ,
, ,
, .
.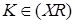 , а
, а  і
і 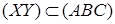 , то
, то  і
і  . Так як
. Так як  , а
, а  , то
, то 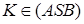 . Таким чином точка
. Таким чином точка 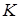 являється спільною точкою площин
являється спільною точкою площин  . Точка
. Точка  також являється спільною точкою площин. Тому
також являється спільною точкою площин. Тому  - пряма, по якій перетинаються січна площина
- пряма, по якій перетинаються січна площина 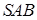 піраміди.
піраміди.
 .
. являються точками, які лежать в січній площині
являються точками, які лежать в січній площині 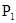 ,
,  і
і  .
. і
і  ,
, ,
, ,
,
 . Дійсно,
. Дійсно,  , тобто
, тобто  , і тому
, і тому  . Але
. Але 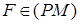 , тобто
, тобто 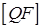 ,
, ,
, .
.




