В основі піраміди 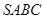 лежить прямокутний трикутник
лежить прямокутний трикутник  . Ребро
. Ребро 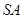 перпендикулярно площині основи,
перпендикулярно площині основи, 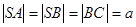 . Через середину ребра
. Через середину ребра 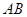 перпендикулярно до ребра
перпендикулярно до ребра 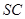 проведемо січну площину і знайдемо площу отриманого перерізу.
проведемо січну площину і знайдемо площу отриманого перерізу.
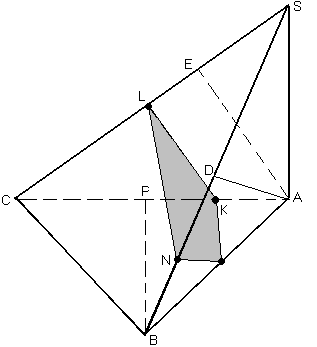
Побудуємо зображення.
Нехай чотирикутник 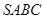 з його діагоналями
з його діагоналями  і
і 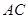 являється зображенням даної піраміди (мал.).
являється зображенням даної піраміди (мал.).
1) 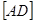 медіана трикутника
медіана трикутника  ,
,
2) точка  - середина ребра
- середина ребра 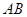 ,
,
3) 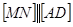 ,
,
4)  - медіана трикутника
- медіана трикутника  ,
,
5) 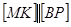 .
.
Для того щоб побудувати  , спочатку побудуємо
, спочатку побудуємо 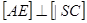 . Зазначимо, що в прямокутному трикутнику
. Зазначимо, що в прямокутному трикутнику 
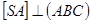 і тому
і тому 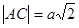 . Тоді з трикутника
. Тоді з трикутника  , де
, де  , знаходимо, що
, знаходимо, що  . Таким чином, для того щоб відрізок
. Таким чином, для того щоб відрізок  було зображенням перпендикуляра до ребра
було зображенням перпендикуляра до ребра 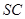 , повинна виконуватись рівність:
, повинна виконуватись рівність:
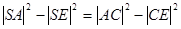 , або
, або 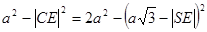 , звідси знаходимо, що
, звідси знаходимо, що 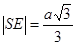 , тобто
, тобто 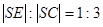 .
.
Далі ми продовжимо побудову в такій послідовності:
6) точка  така, що
така, що 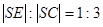 ,
,
7) 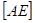 ,
,
8) 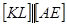 ,
,
9)  .
.
Доведемо, що площина чотирикутника  перпендикулярна ребру
перпендикулярна ребру 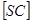 . Дійсно,
. Дійсно, 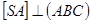 , тобто
, тобто 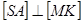 . Крім того, за побудовою
. Крім того, за побудовою  . Тоді
. Тоді  і
і  . Далі
. Далі  і
і 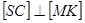 , тобто
, тобто  . Таким чином, переріз
. Таким чином, переріз  задовільняє умовам залачі і, тому, являється шуканим.
задовільняє умовам залачі і, тому, являється шуканим.
Зрозуміло, що так як січна площина перпендикулярна даній прямій і проходить через дану точку, яка належить поверхні піраміди, визначена цими умовами, існує і при тому тільки одна.
Побудову зображення закінчено, і можна перейти до подальших етапів розв’язання.
Дано:
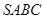 - піраміда,
- піраміда, 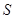 - вершина,
- вершина, 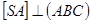 ,
,  ,
, 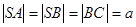 ,
,  ,
, 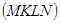 - переріз піраміди,
- переріз піраміди, 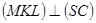 .
.
Знайти: 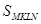
Розв’язання:
Для того щоб розрахувати дану площу, визначимо спочатку вид чотирикутника  .
.
З прямокутних трикутників  і
і  маємо відповідно:
маємо відповідно:
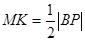 і
і 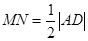 .
.
Але  . Таким чином,
. Таким чином,  .
.
Оскільки 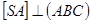 , то
, то 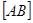 - проекція ребра
- проекція ребра  на площину
на площину  . Але
. Але  . Тоді і
. Тоді і 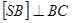 .
.
З подібності трикутників 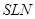 і
і 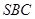
 ,
,
звідси  .
.
З подібності трикутників 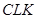 і
і 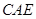

 ,
,
звідси 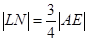 .
.
Але  , тобто
, тобто 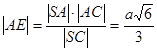 , а тоді
, а тоді  .
.
Таким чином, чотирикутник  має ту особливість, що в нього
має ту особливість, що в нього 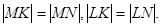
Далі не важко побачити, що трикутники  і
і 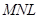 і тому
і тому 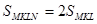 . Але
. Але  і
і  , тобто
, тобто  .
.
Звідси,  ,
,
а тоді, 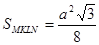 .
.

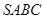 лежить прямокутний трикутник
лежить прямокутний трикутник  . Ребро
. Ребро 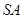 перпендикулярно площині основи,
перпендикулярно площині основи, 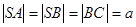 . Через середину ребра
. Через середину ребра 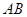 перпендикулярно до ребра
перпендикулярно до ребра 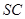 проведемо січну площину і знайдемо площу отриманого перерізу.
проведемо січну площину і знайдемо площу отриманого перерізу. і
і 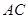 являється зображенням даної піраміди (мал.).
являється зображенням даної піраміди (мал.).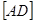 медіана трикутника
медіана трикутника  ,
, - середина ребра
- середина ребра 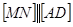 ,
, - медіана трикутника
- медіана трикутника 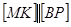 .
. , спочатку побудуємо
, спочатку побудуємо 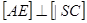 . Зазначимо, що в прямокутному трикутнику
. Зазначимо, що в прямокутному трикутнику 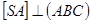 і тому
і тому 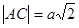 . Тоді з трикутника
. Тоді з трикутника  , де
, де  , знаходимо, що
, знаходимо, що  . Таким чином, для того щоб відрізок
. Таким чином, для того щоб відрізок  було зображенням перпендикуляра до ребра
було зображенням перпендикуляра до ребра 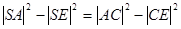 , або
, або 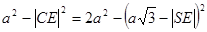 , звідси знаходимо, що
, звідси знаходимо, що 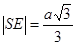 , тобто
, тобто 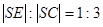 .
. така, що
така, що 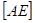 ,
,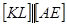 ,
, .
. перпендикулярна ребру
перпендикулярна ребру 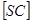 . Дійсно,
. Дійсно, 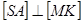 . Крім того, за побудовою
. Крім того, за побудовою  . Тоді
. Тоді  і
і  . Далі
. Далі  і
і 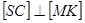 , тобто
, тобто  . Таким чином, переріз
. Таким чином, переріз 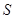 - вершина,
- вершина,  ,
,  ,
, 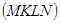 - переріз піраміди,
- переріз піраміди, 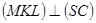 .
.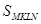

 і
і 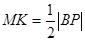 і
і 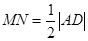 .
. . Таким чином,
. Таким чином,  .
.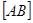 - проекція ребра
- проекція ребра 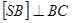 .
.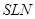 і
і 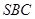
 ,
, .
.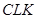 і
і 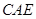

 ,
,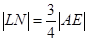 .
. , тобто
, тобто 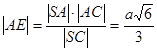 , а тоді
, а тоді  .
.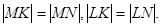
 і
і 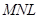 і тому
і тому 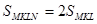 . Але
. Але  і
і  , тобто
, тобто  ,
,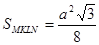 .
.


