В правильній трикутній піраміді 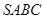 проведено переріз, паралельно ребру
проведено переріз, паралельно ребру  , який проходить через точки
, який проходить через точки  і
і  - середини ребер
- середини ребер 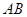 і
і  відповідно.
відповідно.

Розв‘язання.
Нехай чотирикутник  з його діагоналями
з його діагоналями  та
та  являється зображенням даної піраміди (мал. 14). Зрозуміло, що двома точками
являється зображенням даної піраміди (мал. 14). Зрозуміло, що двома точками  і
і  та прямою
та прямою  цілком визначається положення січної площини. Таким чином, задача о побудові перерізу на цьому зображенні виконувана. Перейдемо до зображення січної площини.
цілком визначається положення січної площини. Таким чином, задача о побудові перерізу на цьому зображенні виконувана. Перейдемо до зображення січної площини.
Позначимо січну площину через 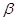 .
.
Так як  ,
,  ,
,  ,
,  , то
, то  ,
,  . Але
. Але  , і
, і  . Тоді
. Тоді  . Далі,
. Далі,
1)  .
.
Так як  , то площина
, то площина  , яка проходить через ребро
, яка проходить через ребро 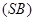 , перетне
, перетне 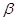 по прямій, яка проходить через точку
по прямій, яка проходить через точку  і паралельній ребру
і паралельній ребру  . Тому
. Тому
2)  . Аналогічно
. Аналогічно
3)  , після цього
, після цього
4)  .
.
Ясно, що чотирикутник  задовольняє умові задачі і тому являється шуканим перерізом. Не важко переконатися, що потрібний переріз існує, при тому тільки один.
задовольняє умові задачі і тому являється шуканим перерізом. Не важко переконатися, що потрібний переріз існує, при тому тільки один.
Зауваження.
Метод відповідності зручно застосовувати тоді, коли слід січної площини у площині основи многогранника або тіл обертання лежить за межами креслення цих фігур. Незручність цього методу полягає в тому, що велика кількість штрихових ліній, які доводиться проводити в процесі розв‘язання задачі, викликає помітні труднощі в читанні креслень.
За допомогою цього ж прикладу розглянемо другий тип задач, тобто задач в умові яких обумовлюється (або мається на увазі), що переріз проведено.
Нехай в прикладі 12 сторона основи піраміди дорівнює  , а бічне ребро дорівнює
, а бічне ребро дорівнює  . Знайдемо площину перерізу.
. Знайдемо площину перерізу.
Для цього нам треба вияснити форму перерізу (вид чотирикутника  ).
).
Так як за побудовою  і
і  , то
, то 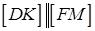 .
. 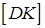 - середня лінія трикутника
- середня лінія трикутника 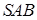 , тобто
, тобто  . Аналогічно
. Аналогічно  , тому
, тому  , и тоді чотирикутник
, и тоді чотирикутник  - паралелограм, причому
- паралелограм, причому 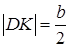 ,
,  . Для знаходження площі паралелограма цих даних, однак, не достатньо, тому уточнимо форму паралелограма
. Для знаходження площі паралелограма цих даних, однак, не достатньо, тому уточнимо форму паралелограма  . Побудуємо
. Побудуємо 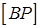 - медіану трикутника
- медіану трикутника  . Ясно, що
. Ясно, що  , точка
, точка  - основа висоти
- основа висоти 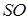 піраміди.
піраміди.
Так як  і
і 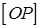 - проекція відрізка
- проекція відрізка  на площину
на площину  , то
, то  (за теоремою о трьох перпендикулярах).
(за теоремою о трьох перпендикулярах).
Таким чином,  і
і  . Але тоді
. Але тоді  . (Ми довели, що мимобіжні ребра правильної трикутної піраміди взаємно перпендикулярні).
. (Ми довели, що мимобіжні ребра правильної трикутної піраміди взаємно перпендикулярні).
Далі, так як  і
і  , то і
, то і  , тобто паралелограм
, тобто паралелограм  - прямокутник.
- прямокутник.
Таким чином отримаємо:
 .
.

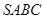 проведено переріз, паралельно ребру
проведено переріз, паралельно ребру  , який проходить через точки
, який проходить через точки  і
і  - середини ребер
- середини ребер 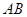 і
і  відповідно.
відповідно.
 з його діагоналями
з його діагоналями  та
та 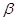 .
. ,
,  ,
,  ,
,  , то
, то  ,
,  . Але
. Але  , і
, і  . Тоді
. Тоді  . Далі,
. Далі, .
. , то площина
, то площина  , яка проходить через ребро
, яка проходить через ребро 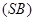 , перетне
, перетне  . Аналогічно
. Аналогічно , після цього
, після цього .
. задовольняє умові задачі і тому являється шуканим перерізом. Не важко переконатися, що потрібний переріз існує, при тому тільки один.
задовольняє умові задачі і тому являється шуканим перерізом. Не важко переконатися, що потрібний переріз існує, при тому тільки один. , а бічне ребро дорівнює
, а бічне ребро дорівнює  . Знайдемо площину перерізу.
. Знайдемо площину перерізу. і
і  , то
, то 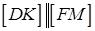 .
. 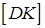 - середня лінія трикутника
- середня лінія трикутника 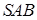 , тобто
, тобто  . Аналогічно
. Аналогічно  , тому
, тому  , и тоді чотирикутник
, и тоді чотирикутник 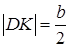 ,
,  . Для знаходження площі паралелограма цих даних, однак, не достатньо, тому уточнимо форму паралелограма
. Для знаходження площі паралелограма цих даних, однак, не достатньо, тому уточнимо форму паралелограма 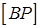 - медіану трикутника
- медіану трикутника  . Ясно, що
. Ясно, що  , точка
, точка  - основа висоти
- основа висоти 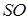 піраміди.
піраміди. і
і 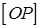 - проекція відрізка
- проекція відрізка  на площину
на площину  (за теоремою о трьох перпендикулярах).
(за теоремою о трьох перпендикулярах). і
і  . Але тоді
. Але тоді  . (Ми довели, що мимобіжні ребра правильної трикутної піраміди взаємно перпендикулярні).
. (Ми довели, що мимобіжні ребра правильної трикутної піраміди взаємно перпендикулярні). і
і  , то і
, то і  , тобто паралелограм
, тобто паралелограм  .
.


