Слідом січної площини називають пряму, утриману при перетині січної площини з якою-небудь площиною, яка задана на зображенні.
Цей метод полягає в побудові слідів площини перерізу на гранях даної фігури.
Приклад 9. Побудувати лінію перетину (слід) площини  з основною площиною
з основною площиною  , якщо площина
, якщо площина  задана точками
задана точками  які не належать площині
які не належать площині  .
.  - проекції точок
- проекції точок  на площину
на площину  .
.
Розв‘язання.
 Коли дві площини мають спільну точку, то вони перетинаються по прямій. Отже треба побудувати такі дві точки
Коли дві площини мають спільну точку, то вони перетинаються по прямій. Отже треба побудувати такі дві точки  та
та  , які визначають єдину пряму
, які визначають єдину пряму  , що належить площині
, що належить площині  (мал. 27). Такими точками будуть точки перетину прямих
(мал. 27). Такими точками будуть точки перетину прямих  і
і  з пл.
з пл.  . З цього випливає така побудова: визначаємо точку
. З цього випливає така побудова: визначаємо точку  , в якій пряма
, в якій пряма  перетинає площину проекцій
перетинає площину проекцій  , і точку
, і точку  , в якій пряма
, в якій пряма  перетинає ту саму пл.
перетинає ту саму пл.  . Оскільки знайдені точки
. Оскільки знайдені точки  та
та  одночасно належать і площині
одночасно належать і площині  , і площині
, і площині  , і ці точки різні, то
, і ці точки різні, то  - шукана пряма, яка і слідом перетину площини
- шукана пряма, яка і слідом перетину площини  і площини
і площини  .
.
Зауваження.
Пряма  - не лише слід, а й носій точок перетину нескінченої сукупності прямих, які належать площині
- не лише слід, а й носій точок перетину нескінченої сукупності прямих, які належать площині  і перетинають основну площину
і перетинають основну площину  . Це положення є одним з головних під час розв‘язання задач на побудову перерізів геометричних тіл методом слідів.
. Це положення є одним з головних під час розв‘язання задач на побудову перерізів геометричних тіл методом слідів.
Розв‘яжемо кілька задач на побудову перерізів геометричних тіл методом слідів.
Приклад 10. На ребрах куба  дані точки
дані точки  ,
,  і
і  такі, що
такі, що  ,
,  і
і  . Побудувати переріз куба площиною
. Побудувати переріз куба площиною  .
.
Розв‘язання:
Вияснимо спочатку, чи має розв’язок ця задача. Нехай фігура  являється зображенням куба (мал. 28). Це зображення повне. Зрозуміло також, що, маючи на зображенні точки
являється зображенням куба (мал. 28). Це зображення повне. Зрозуміло також, що, маючи на зображенні точки  ,
,  і
і  - проекції точок
- проекції точок  ,
,  і
і  ми можемо знайти і вторинні проекції точок
ми можемо знайти і вторинні проекції точок  ,
,  і
і  . Для цього достатньо виконати в площині зображення внутрішнє паралельне проектування, наприклад, в направленні паралельному (
. Для цього достатньо виконати в площині зображення внутрішнє паралельне проектування, наприклад, в направленні паралельному ( ). Таким чином ми знайдемо точки
). Таким чином ми знайдемо точки  ,
,  і
і  і прийдемо до висновку, що зображення січної площини являється заданим. Тоді задача о знаходженні перетину площини заданої точками
і прийдемо до висновку, що зображення січної площини являється заданим. Тоді задача о знаходженні перетину площини заданої точками  ,
,  і
і  з поверхністю куба розв'язана.
з поверхністю куба розв'язана.
Перейдемо безпосередньо до побудови перерізу (звичайно говорять о побудові перерізу, хоча мова йде о побудові зображення перерізу). Перший етап в загальній схемі розв‘язання задачі на побудову – аналіз – у розглянутому прикладі опускається, а другий і третій етапи – побудова та доведення – проводяться одночасно.
По-перше знайдемо слід січної площини – лінію перетину площини  з площиною
з площиною  .
.
1)  .
.
Так як  , а
, а  , то
, то  . Так як
. Так як  , а
, а  , то
, то  . Таким чином точка
. Таким чином точка  являється спільною точкою двох площин
являється спільною точкою двох площин  та
та  . Точка
. Точка  також являється спільною точкою двох площин. Тоді
також являється спільною точкою двох площин. Тоді  - пряма, по якій перетинаються площини
- пряма, по якій перетинаються площини  та
та  ,
,  тобто
тобто
2)  - слід січної площини.
- слід січної площини.
Далі: 3)  ,
,
4)  ,
,
5)  .
.
Так як  , а
, а  і
і  , то
, то  і
і  . Так як
. Так як 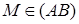 , а
, а  , то
, то 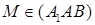 . Таким чином точка
. Таким чином точка  являється спільною точкою площин
являється спільною точкою площин  і
і  . Точка
. Точка  також являється спільною точкою площин. Тому
також являється спільною точкою площин. Тому  - пряма, по якій перетинаються січна площина
- пряма, по якій перетинаються січна площина  з площиною бокової грані
з площиною бокової грані  куба.
куба.
6)  ,
,
7)  ,
,
8) 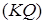 .
.
Аналогічно знаходимо точку  та виконуємо подальші побудови:
та виконуємо подальші побудови:
9)  ,
,
10)  ,
,
11)  .
.

Оскільки за побудовою вершини многокутника  являються точками, які лежать в січній площині
являються точками, які лежать в січній площині  і належать ребрам куба, то многокутник
і належать ребрам куба, то многокутник  - шуканий переріз.
- шуканий переріз.
Так як за змістом задачі точки  ,
,  і
і  не лежать на даній прямій, то задача має єдине рішення.
не лежать на даній прямій, то задача має єдине рішення.
Змінемо умову задачі.

 з основною площиною
з основною площиною  , якщо площина
, якщо площина  які не належать площині
які не належать площині  - проекції точок
- проекції точок  на площину
на площину  Коли дві площини мають спільну точку, то вони перетинаються по прямій. Отже треба побудувати такі дві точки
Коли дві площини мають спільну точку, то вони перетинаються по прямій. Отже треба побудувати такі дві точки  та
та  , які визначають єдину пряму
, які визначають єдину пряму  , що належить площині
, що належить площині  і
і  з пл.
з пл.  .
. дані точки
дані точки  ,
,  і
і  такі, що
такі, що  ,
,  і
і  . Побудувати переріз куба площиною
. Побудувати переріз куба площиною  .
. ,
,  і
і  ми можемо знайти і вторинні проекції точок
ми можемо знайти і вторинні проекції точок  ). Таким чином ми знайдемо точки
). Таким чином ми знайдемо точки  ,
,  і
і  і прийдемо до висновку, що зображення січної площини являється заданим. Тоді задача о знаходженні перетину площини заданої точками
і прийдемо до висновку, що зображення січної площини являється заданим. Тоді задача о знаходженні перетину площини заданої точками  .
. .
. , а
, а  , то
, то  . Так як
. Так як  , а
, а  , то
, то  . Таким чином точка
. Таким чином точка  та
та  також являється спільною точкою двох площин. Тоді
також являється спільною точкою двох площин. Тоді  - пряма, по якій перетинаються площини
- пряма, по якій перетинаються площини  тобто
тобто ,
, ,
, .
. , а
, а  і
і  , то
, то  і
і  . Так як
. Так як 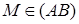 , а
, а  , то
, то 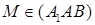 . Таким чином точка
. Таким чином точка  являється спільною точкою площин
являється спільною точкою площин  . Точка
. Точка  також являється спільною точкою площин. Тому
також являється спільною точкою площин. Тому  - пряма, по якій перетинаються січна площина
- пряма, по якій перетинаються січна площина  куба.
куба. ,
, ,
,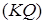 .
. та виконуємо подальші побудови:
та виконуємо подальші побудови: ,
, ,
, .
.

 являються точками, які лежать в січній площині
являються точками, які лежать в січній площині  і належать ребрам куба, то многокутник
і належать ребрам куба, то многокутник  ,
,  і
і  не лежать на даній прямій, то задача має єдине рішення.
не лежать на даній прямій, то задача має єдине рішення.


