Властивості проекцій.
Щоб грамотно будувати зображення геометричної фігури в центральній чи паралельній проекціях, треба знати властивості цих проекцій. Центральна проекція має властивості, які випливають з описаного способу побудови. 1. Проекцією точки є точка. 2. За даних умов проектування (задані площина Проектування можна виконати для будь-якої точки простору, за винятком точок, що лежать у площині, яка проходить через центр проекцій Означення. Пряма, похилена до площини називається прямою загального положення. 3. Поекцією прямої загального положення є пряма (мал. 5). Справді, площина, яка визначається точкою 4. Якщо точка належить будь-якій лінії (прямій чи кривій), то проекція цієї точки належить проекції цієї лінії, тобто, якщо
Паралельна проекція має властивості, які випливають з описаного способу побудови. 1. Проекцією точки є точка. 2. За даних умов проектування (задані площина Справді, через точку, що не лежить на даній прямій, можна провести на площині на більше як одну пряму, паралельну даній (аксіома паралельних прямих). 3. Проекцією прямої загального положення є пряма. Справді, нехай Якщо пряма паралельна напряму 4. Проекції паралельних прямих паралельні. Так площини
5. При паралельному проектуванні відношення відрізків однієї прямої або паралельних прямих дорівнює відношенню проекцій відповідних відрізків (мал. 9). Наслідок. Середина відрізка прямої при паралельному проектуванні проектується в середину проекції цього відрізка. 6. Якщо точка належить прямій, то проекція цієї точки належить проекції даної прямої. Ця властивість, яку називають властивістю належності, випливає з означення проекції фігури як сукупності проекцій усіх її точок. 7. Якщо відрізок Справді, нехай
Тобто можна зробити такі висновки. Зображення побудова в центральній або паралельній проекціях, мають свої позитивні якості та свої недоліки. Наше око бачить всі предмети в центральній проекції. Вона дає чудове загальне уявлення про зображені предмети. Але її властивості та закони її побудови досить складні і це створює певні труднощі для детального вивчення зображених предметів за їх зображенням. Ці проекції використовуються, наприклад, архітектурі, коли треба виконати зображення населених пунктів та будівель. Стосовно паралельної проекції, то ми ніколи не бачимо предмети такими, якими вони зображуються в цій проекції. Проте її властивості і закони її побудови простіші ніж для центрального проекції. Через те паралельна проекція (а точніше – ортогональна проекція) широко використовується в техніці. Всі технічні креслення виконуються в ортогональній проекції. Співставлення та протиставлення центрального та ортогонального способів проектувань легко показує те спільне і відмінне, що їм притаманне, спільні і відмінні властивості відповідних проекцій. Учні приходять до висновку про незмінні властивості проектуючих об’єктів відносно проекційних відображень:
a) Проекцією точки є точка. b) Проекцією прямої (в загальному випадку) є пряма. c) Якщо пряма паралельна напряму При розгляді властивостей паралельно проектування, слід звернути увагу учнів на зображення взаємозалежності точки і прямої. Із властивості збереження при паралельному проектуванні випливає досить важливий наслідок: проекція середини відрізка-оригіналу є серединою його проекції на площину (тобто середина переходить у середину). У підсумковій бесіді з учнями доцільно розглянути проектування на площину кривих ліній. Внаслідок чого центральне проектування інколи називають – конічним, а паралельне – циліндричним. Поняття проекційного креслення можна дати учням після вивчення аксіом стереометрії та їх наслідків, перпендикулярності та паралельності прямих та площин. Тільки після цього можна перейти до розв’язання відповідних стереометричних задач на побудову.
|

 і центр
і центр  проектування) кожна точка простору за винятком точки
проектування) кожна точка простору за винятком точки  , перетинає площину проекцій
, перетинає площину проекцій  . Якщо пряма проходить через центр
. Якщо пряма проходить через центр  , то
, то  (мал. 6).
(мал. 6).
 проектування), кожна точка простору, яка не належить напряму
проектування), кожна точка простору, яка не належить напряму  і
і  - дві різні точки даної прямої
- дві різні точки даної прямої 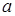 і
і 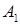 та
та  точок
точок  та
та  . Через те, що
. Через те, що 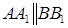 , то через прямі
, то через прямі 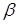 . Тоді
. Тоді  і
і  (мал. 8) проведені в просторі через паралельні прямі
(мал. 8) проведені в просторі через паралельні прямі  , паралельні між собою. Ці площини перетинаються третьою (у даному випадку площиною
, паралельні між собою. Ці площини перетинаються третьою (у даному випадку площиною  і
і  , які паралельні між собою.
, які паралельні між собою.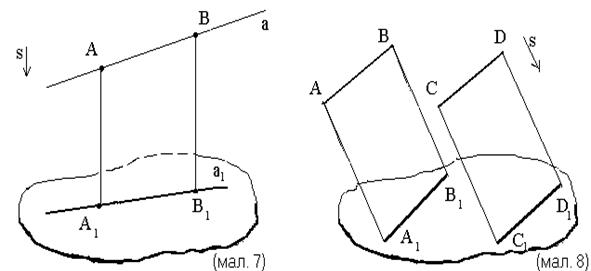
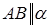 , тоді відрізок
, тоді відрізок 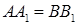 , де
, де 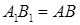 .
.



