Приклад 1.
Побудувати площину, паралельну даній площині Розв‘язання. Нехай точка 1) 2) через пряму 3) в площині 4) через пряму 5) в площині
6) через прямі, які перетинаються Площина Наведені операції не тільки не виконуються, але деякі з них навіть не можуть бути виконаними. Справді, якщо прямі З наведеного приклада можна побачити, що в уяві утримуються не тільки задані елементи, але й елементи отримані в процесі побудови, а також розв’язуванні задачі. В цьому випадку уявлюваною являється і сама побудова. Креслення при розв‘язанні задач на побудову може й не виконуватися. У тих же випадках, коли його застосовують, воно грає допоміжну роль: креслення необхідне для полегшення праці уяви, коли просторова уява погано розвинена або, коли побудови виявляються громіздкими. У курсі геометрії середньої школи задачі на побудову розв‘язуються переважно в уяві. Такий підхід до розв’язання задачі на побудову становить деякий інтерес. У процесі розв‘язування задач на побудову розвивається просторова уява, це в свою чергу полегшує учням проходження всього останнього навчального матеріалу. В цей же час необхідно мати на увазі, що оволодіння методами розв‘язування задач на побудову допускає вже достатньо високий рівень розвитку просторової уяви учнів. Крім того, розв‘язування задач на побудову при традиційній методі закінчуються доведенням існування та єдиності розв‘язку і не доводиться до фактичного відшукання розв’язання побудовою, як це робиться, наприклад, у планіметрії, коли практична ціль задачі на побудову в планіметрії та стереометрії складається з відшукання розв‘язку фактичною побудовою інструментами. Відмічені недоліки традиційної системи навчання розв‘язуванню задач вдається заповнити при навчанні учнів розв’язанню задач на побудову на проекційному кресленні.
|

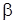 , яка проходить через дану точку
, яка проходить через дану точку 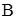 .
.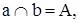
 ,
,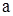 і точку
і точку 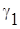 ,
,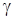 , через точку
, через точку 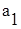 , паралельну прямій
, паралельну прямій 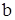 і точку
і точку 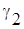 ,
,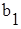 , паралельну прямій
, паралельну прямій 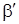 .
.


