Приклад 13.
Побудувати переріз циліндра (конуса) площиною, заданою трьома точками, дві з яких належать бічній поверхні, а третя розміщена поза циліндром (конусом). Розв’язання. Нехай заданими точками будуть
Будуємо слід 1. 2. 3. 4. 5.
Точка 6. 7. 8. 9. 10. 11. Сполучивши плавною кривою точки 1. Задача на побудову точки перетину прямої з площиною є основою методу розв‘язання задач на побудову перерізів многогранників та тіл обертання методом слідів. 2. Побудова сліду (прямої) перетину січної площини якщо його не задано з основною площиною є головним етапом в розв‘язанні задач на знаходження лінії перерізу. 3. Побудова сліду можлива, якщо задана січна площина не паралельна основній площині і не виходить за межі аркуша паперу.
|

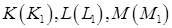 дві з яких
дві з яких 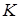 і
і  розміщені на поверхні циліндра (мал. 31), (для конуса мал. 32), а точка
розміщені на поверхні циліндра (мал. 31), (для конуса мал. 32), а точка 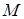 - поза циліндром (конусом).
- поза циліндром (конусом).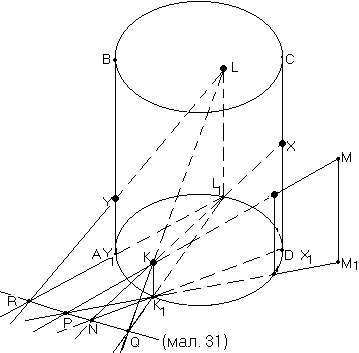

 перетину січної площини з площиною основи циліндра (конуса):
перетину січної площини з площиною основи циліндра (конуса):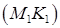 ,
, 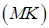 ,
, 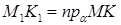 ,
, .
.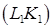 ,
,  ,
,  ,
,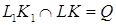 ,
,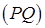 .
.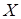 і
і 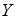 , які належать контурним твірним циліндра (конуса), їх проекції на площину наперед знаємо. Для циліндра:
, які належать контурним твірним циліндра (конуса), їх проекції на площину наперед знаємо. Для циліндра:  ,
, 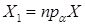 ,
, 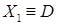 .
. 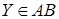 ,
, 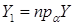 ,
, 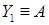 .
.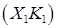 ,
,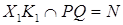 ,
,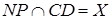 .
.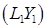 ,
,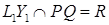 ,
, .
.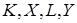 , дістанемо шукану лінію перерізу – еліпс.
, дістанемо шукану лінію перерізу – еліпс.


