Анализ устойчивости с использованием частотного критерия (критерия Михайлова).
Данный метод заключается в построении годографа Михайлова, который определяет устойчивость САУ по характеру обхода этим годографом необходимого числа квадрантов. Метод основан на характеристическом уравнении системы замкнутого типа. Характеристическое уравнение системы замкнутого типа имеет вид:
где
Заменим в уравнении
оператор Лапласа [p] на Получим:
При этом учтём, что
Вещественная составляющая равна:
Мнимая (комплексная) составляющая:
Для построения годографа Михайлова построим таблицу значений при частоте, изменяющейся от 0 до +¥:
Построим годограф Михайлова и проанализируем устойчивость, исходя из графика:
Итак, годограф начинается на вещественной положительной оси, но при изменении частоты w от 0 до +¥ он не обходит последовательно 4 квадранта координатной плоскости, а переходит из первой четверти сразу в четвертую, и стремится к ¥ по оси абсцисс и -¥ по оси ординат, что не характерно для устойчивых систем. Следовательно, система неустойчива.
3.3) Анализ влияния Значение
|
,
.
; 
; 
; 
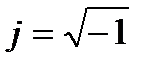разомкнутой САУ на устойчивость
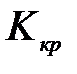можно найти из определителя Гурвица. Для этого нужно приравнять диагональный минор наименьшего порядка, содержащий в своих коэффициентах 
, т.к. 
и 
содержат 
(
)- 
;
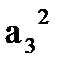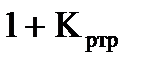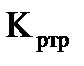
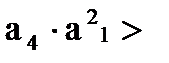
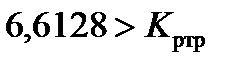