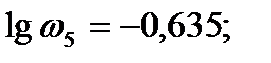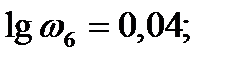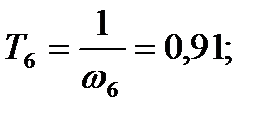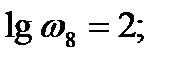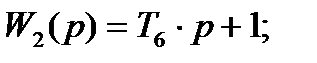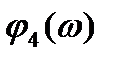Выбор и обоснование методов синтеза САУ
Асимптотические логарифмические амплитудно-частотные и фазочастотные характеристики строятся очень просто и поэтому широко используются при инженерных расчётах. По этим характеристикам можно не только проверить устойчивость системы, но и произвести ее оценку качества.
4.2) Расчёт и построение желаемой ЛАХ и ФЧХ Построение желаемой ЛАХ: Следуя предписаниям учебника [2] на страницах 228-230 наша желаемая ЛАХ имеет три части: низкочастотную, среднечастотную и высокочастотную. Низкочастотная часть желаемой ЛАХ похожа на низкочастотную часть исходной. Высокочастотная часть желаемой ЛАХ может быть произвольной, т.к. на никакие качества системы не влияет. Среднечастотная часть желаемой ЛАХ требует детальных расчётов. · Найдём частоту среза.
где
Используем номограмму В. В. Солодовникова. От шкалы перерегулирования проводим линии (как на рисунке) и находим значения c=2.9 и Рмах=1,18 Находим значение частоты среза:
· Определим протяженность среднечастотной части ЛАХ. Для этого воспользуемся второй номограммой.
Проведя с оси Pmax из точки с найденным нами значением линии, как показано на рисунке (красные стрелки), находим запас по фазе Графическое построение ЛАХ: 1) Прочертим едва видные горизонтали 2) Сопрягающую НЧ и СЧ части асимптоту проведём с наклоном 3) Высокочастотную асимптоту сделаем с наклоном
Построение желаемой ФЧХ: Первоначально запишем ПФ желаемой САУ по построенной ЛАХ. Сначала она имеет нулевой наклон с усиление 42,79 дБ, потом доходя до частоты
· Находим постоянные времени.
· Разбиваем ПФ на элементарные звенья.
· Для каждого звена определим аналитическое выражение для ФЧХ.
· Определяем значения для ФЧХ и строим ее.
|



 - время регулирования (заранее заданное), c – некая константа.
- время регулирования (заранее заданное), c – некая константа.

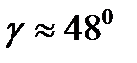 и численное значение верхнего и нижнего пределов среднечастотной части LM=16.
и численное значение верхнего и нижнего пределов среднечастотной части LM=16. и
и  (Приложение 1). Возьмём наклон среднечастотной части желаемой ЛАХ
(Приложение 1). Возьмём наклон среднечастотной части желаемой ЛАХ  и проведём её через частоту среза, до горизонталей
и проведём её через частоту среза, до горизонталей  из конца СЧ асимптоты до пересечения с НЧ асимптотой исходной ЛАХ.
из конца СЧ асимптоты до пересечения с НЧ асимптотой исходной ЛАХ. и проведём её из другого конца СЧ асимптоты, а при
и проведём её из другого конца СЧ асимптоты, а при  сделаем наклон
сделаем наклон  .
. ломается на
ломается на  она поднимается на
она поднимается на 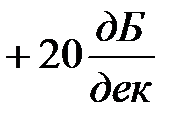 . При частоте
. При частоте  она ломается на
она ломается на  , и при частоте
, и при частоте  еще на
еще на  . Из этого следует передаточная функция:
. Из этого следует передаточная функция: