Построение проектируемой зубчатой передачи.
Примем масштаб: Порядок построения проектируемой зубчатой передачи:
2) Через полюс зацепления касательно к основным окружностям проведена линия зацепления. Точки касания N1 и N2 называются предельными точками линии зацепления. Построенная линия образует с перпендикуляром, восстановленным к осевой линии в полюсе, угол зацепления
3) На шестерне построим четыре зуба, а на колесе три, причем точка контакта К расположена на активной линии зацепления. Профиль шестерни 1 получен программными методами из зубьев, полученных в станочном зацеплении. Так как у нас имеют место два совершенно одинаковых зубчатых колеса, то и профиль колеса получен аналогично.
4) На чертеже указаны диаметры начальных, делительных, основных окружностей, окружности вершин и впадин, шаг и толщина зубьев по делительным окружностям, высота зуба, межосевое расстояние, воспринимаемое смещение, угол зацепления, радиальный зазор, положения профилей в точках начала и конца зацепления, углы торцевого перекрытия.
Проектирование планетарного редуктора с цилиндрическими колесами.
При кинематическом синтезе планетарной зубчатой передачи необходимо выполнить следующие условия: 1) выполнения заданного передаточного отношения;
Если задано передаточное отношение от водила к колесу, а не наоборот, можно использовать формулу:
2) отсутствия заклинивания передачи, среза и подреза профилей зубьев колес; Для исключения подрезания и заклинивания принимают для колес с внешним зацеплением: Для колес с внутренним зацеплением:
3) соосности входного и выходного валов – определяется соосное расположение центральных колес планетарного механизма с водилом Н; 4) соседства – учитывает возможность свободного размещения сателлитов без соприкосновения их друг с другом;
5) сборки – если один из сателлитов свободно устанавливается на вертикальной оси, то все последующие сателлиты будут свободно входить в зацепление с соответствующими колесами в той же позиции.
водила при сборке. Ц-любое целое число. Заданная планетарная коробка передач состоит из однорядного планетарного редуктора смешанного зацепления с тремя сателлитами. При проектировании редуктора используем следующие исходные данные: Передаточное отношение: Число сателлитов: k = 3. Задача определения числа зубьев сведена к составлению исходных уравнений, отражающих указанные условия и требования. Одним из наиболее распространённых методов определения числа зубьев является метод сомножителей, но в случае однорядного планетарного редуктора задача по нахождению числе зубьев решается без применения данного метода. Произведём расчёт передаточного отношения планетарной передачи. Для вывода формулы передаточного отношения воспользуемся методом Виллиса (метод обращения движения), согласно которому всем звеньям задана угловая скорость –ωH при условно остановленном водиле. Тогда получим: Таблица 3.1.
Получен обращенный механизм.
Из условия соосности
Из условия отсутствия подрезания: z12, z13 ≥ zmin = 17; z14 ≥ zmin = 85. Примем z12=20, тогда z13=40 z14=100. Проектируемый редуктор удовлетворяет следующим требованиям: Обеспечивает необходимое передаточное отношение. 1) необходимое передаточное отношение 2) Соблюдено условие соосности: z12+z13=z14-z13 20+40=100-40 60=60 – условие соосности выполнено. 3) Выполнено условие соседства (совместности), т.е. есть возможность размещения нескольких сателлитов по общей окружности в одной плоскости без соприкосновения друг с другом.
0,866>0,7 – условие совместности выполнено. 4) Соблюдено условие сборки, т.е. обеспечена возможность одновременного зацепления всех сателлитов с центральными колесами при равных углах между сателлитами:
при любом целом П. 5) Соблюдено условие отсутствия подрезания, т.е. при колесах, нарезанных стандартным инструментом без смещения (при z12, z13 ≥ zmin = 17; z14 ≥ zmin = 85. Все условия выполнены. Определим значение модуля. Из первого листа возьмем наибольший приведенный суммарный движущий момент
В соответствии со стандартным рядом модулей принимаем m=2,5мм.
Рассчитаны радиусы колес в планетарном редукторе:
|

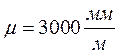
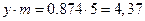 . Расстояние между окружностями вершин одного колеса и впадин другого, измеренного по осевой линии, равно радиальному зазору
. Расстояние между окружностями вершин одного колеса и впадин другого, измеренного по осевой линии, равно радиальному зазору 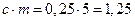 .
. . Отметим точки В1 и В2. Точка В1 – точка пересечения окружности вершин колеса с линией зацепления. Точка В2- точка пересечения окружности вершин с шестерни с линией зацепления. Линия, соединяющая эти точки, В1В2 - активная линия зацепления. Точка В1 (В2)-точка начала (конца) зацепления.
. Отметим точки В1 и В2. Точка В1 – точка пересечения окружности вершин колеса с линией зацепления. Точка В2- точка пересечения окружности вершин с шестерни с линией зацепления. Линия, соединяющая эти точки, В1В2 - активная линия зацепления. Точка В1 (В2)-точка начала (конца) зацепления.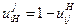 ,где
,где 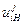 - передаточное отношение числа зубьев i-го колеса к числу зубьев водила Н при неподвижном j-м колесе;
- передаточное отношение числа зубьев i-го колеса к числу зубьев водила Н при неподвижном j-м колесе;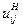 - передаточное отношение числа зубьев i-го колеса к числу зубьев j-го колеса при неподвижном водиле.
- передаточное отношение числа зубьев i-го колеса к числу зубьев j-го колеса при неподвижном водиле.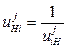
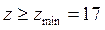 .
.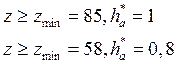
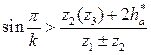 , где k-число сателлитов,z2(z3) -число зубьев большего сателлита,
, где k-число сателлитов,z2(z3) -число зубьев большего сателлита, 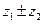 - относительное межосевое расстояние.
- относительное межосевое расстояние.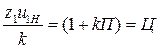 ,где П- произвольное дополнительное число оборотов
,где П- произвольное дополнительное число оборотов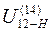 = 6
= 6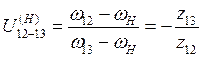
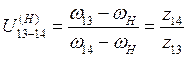
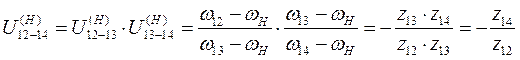 ;
;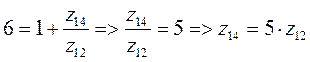
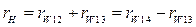 при равных модулях следует, что:
при равных модулях следует, что: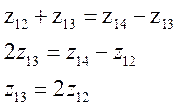
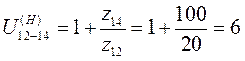
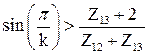
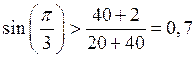
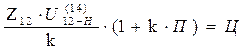 , где Ц – целое число; П=0;1;2...
, где Ц – целое число; П=0;1;2...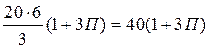 - условие сборки выполняется
- условие сборки выполняется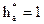 ;
; 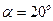 ),
),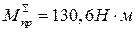 .
.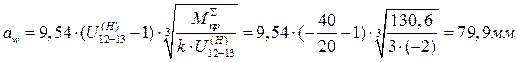 .
.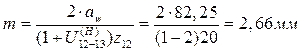
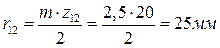 ,
,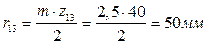 ,
,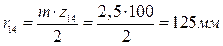 .
.


