Определение 5. Функциональный ряд вида
 , (10)
, (10)
где  последовательность вещественных чисел, называется степенным рядом, а
последовательность вещественных чисел, называется степенным рядом, а 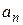 – коэффициентами степенного ряда.
– коэффициентами степенного ряда.
Сразу отметим, что (10) сходится всегда в точке 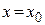 . Рассмотрим верхний предел
. Рассмотрим верхний предел  .
.
Обозначим 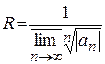 . Будем считать, что если
. Будем считать, что если  , то
, то  , а если
, а если 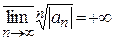 , то
, то  .
.
Теорема 8. (Коши-Адамара). Степенной ряд абсолютно сходится при всех 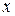 , удовлетворяющих условию
, удовлетворяющих условию  . Если
. Если 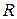 конечное число, то он расходится
конечное число, то он расходится  .
.
‰ Пусть  – конечный, и выполняется неравенство
– конечный, и выполняется неравенство  , тогда
, тогда
 .
.
Выберем число 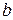 такое, что
такое, что
 .
.
Из определения верхнего предела следует, что неравенство  может не выполниться лишь для конечного числа номеров
может не выполниться лишь для конечного числа номеров  . Поэтому существует такой номер
. Поэтому существует такой номер  , что
, что  выполняется
выполняется
 ,
,
или
 , при
, при  . (11)
. (11)
По признаку сравнения из (11) следует абсолютная сходимость ряда (10). Так как ряд  сходится, как геометрическая прогрессия
сходится, как геометрическая прогрессия  , то ряд
, то ряд  тоже сходится, по признаку Вейерштарсса.
тоже сходится, по признаку Вейерштарсса.
Пусть теперь  , тогда
, тогда  и получаем
и получаем  . Выберем число
. Выберем число 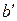 , такое, чтобы
, такое, чтобы
 . (12)
. (12)
В силу теоремы Больцано-Вейерштрасса существует подпоследовательность  сходящаяся к
сходящаяся к  . Тогда из определения предела и неравенства (12) следует, что существует такой номер
. Тогда из определения предела и неравенства (12) следует, что существует такой номер  , что при
, что при 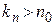 выполняется
выполняется  . Откуда
. Откуда
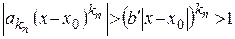
и, следовательно,  при
при 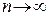 , т.е. нарушено необходимое условие сходимости ряда. ■
, т.е. нарушено необходимое условие сходимости ряда. ■
Итак, если предел конечен, то степенной ряд абсолютно сходится при  и расходится при
и расходится при  .
.
 (13)
(13)
Число R называется радиусом сходимости степенного ряда. Формула (13) называется формулой Коши - Адамара.
Из теоремы следует, что при  ряд сходится только в одной точке
ряд сходится только в одной точке 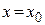 . При
. При  ряд сходится в интервале
ряд сходится в интервале  , а при
, а при  ряд сходится для
ряд сходится для  . Таким образом, областью сходимости степенного ряда является интервал. В граничных точках
. Таким образом, областью сходимости степенного ряда является интервал. В граничных точках  и
и  ряд может и сходится и расходится, поэтому требуется дополнительное исследование. Формулу (13) используют для нахождения радиуса сходимости степенного ряда. Для определения интервала сходимости на практике часто также удобно использовать признак Даламбера для ряда составленного из модулей членов исходного степенного ряда.
ряд может и сходится и расходится, поэтому требуется дополнительное исследование. Формулу (13) используют для нахождения радиуса сходимости степенного ряда. Для определения интервала сходимости на практике часто также удобно использовать признак Даламбера для ряда составленного из модулей членов исходного степенного ряда.
Пример 15. Найти интервал сходимости ряда  .
.
Решение. Найдем величину радиуса сходимости.

 ,
,
 .
.
Так как  , то
, то 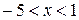 . Таким образом, интервал сходимости ряда
. Таким образом, интервал сходимости ряда  используем сходимость на концах интервала. При
используем сходимость на концах интервала. При  получаем числовой ряд
получаем числовой ряд  , а при
, а при 
 оба ряда сходятся, причем первый сходится абсолютно, как обобщенный гармонический ряд.
оба ряда сходятся, причем первый сходится абсолютно, как обобщенный гармонический ряд.
Теорема 9. (теорема Абеля). Если степенной ряд сходится в точке 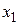 , то он абсолютно сходится для
, то он абсолютно сходится для  .
.
‰ Пусть 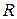 – радиус сходимости ряда (10). Тогда
– радиус сходимости ряда (10). Тогда 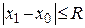 . Это так, потому что, если
. Это так, потому что, если  , то по теореме 8 степенной ряд расходится в точке
, то по теореме 8 степенной ряд расходится в точке 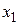 , что противоречит условию. Итак
, что противоречит условию. Итак 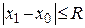 .
.
В силу теоремы 8 ряд (10) сходится при  , а следовательно и при
, а следовательно и при  . <
. <
Теорема10. (о равномерной сходимости степенного ряда). Степенной ряд (10) равномерно сходится на любом отрезке  , содержащимся в интервале сходимости.
, содержащимся в интервале сходимости.
‰ Поскольку отрезок  содержится в интервале сходимости степенного ряда, то в силу теоремы 8 ряд (10) сходится абсолютно в точке
содержится в интервале сходимости степенного ряда, то в силу теоремы 8 ряд (10) сходится абсолютно в точке  , т.е. числовой ряд
, т.е. числовой ряд  – сходится.
– сходится.
Для  выполняется
выполняется  , но так как
, но так как  – сходится, то по признаку Вейерштрасса равномерно сходится ряд (10) на
– сходится, то по признаку Вейерштрасса равномерно сходится ряд (10) на  . <
. <
Теорема 11. Степенной ряд (10) можно почленно дифференцировать и интегрировать в интервале сходимости.
‰ Степенной ряд
 , (14)
, (14)
полученный дифференцированием, имеет тот же интервал сходимости, что и ряд (10). Действительно,
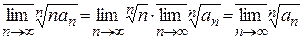 .
.
Отсюда в силу формулы Коши-Адамара следует, что ряды (10) и (14) имеют одинаковые радиусы сходимости. Пусть 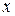 принадлежит интервалу сходимости. Выберем отрезок
принадлежит интервалу сходимости. Выберем отрезок  так, чтобы
так, чтобы  . По теореме 10 ряд сходится равномерно на
. По теореме 10 ряд сходится равномерно на  и в силу теоремы его можно почленно дифференцировать на
и в силу теоремы его можно почленно дифференцировать на  , а, следовательно, и в интервале сходимости. Аналогично доказывается возможность интегрирования. <
, а, следовательно, и в интервале сходимости. Аналогично доказывается возможность интегрирования. <
Это теорема используется для представления функций в виде степенных рядов.
Пример 14. Найти разложение в ряд по степеням 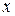 функции
функции  .
.
Решение. Найдем производную, а затем проинтегрируем в интервале сходимости.
 , при
, при 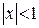 .
.
 ,
, 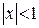 .
.
Пример 15. Найти разложение функции  в степенной ряд.
в степенной ряд.
Решение. Запишем сумму бесконечно убывающей прогрессии со знаменателем 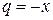
 .
.
Проинтегрируем левую и правую части этого равенства в интервале сходимости 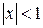
 .
.
Получили представление функции  по степеням
по степеням 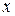 в интервале
в интервале  .
.

 , (10)
, (10) последовательность вещественных чисел, называется степенным рядом, а
последовательность вещественных чисел, называется степенным рядом, а 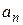 – коэффициентами степенного ряда.
– коэффициентами степенного ряда.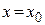 . Рассмотрим верхний предел
. Рассмотрим верхний предел  .
.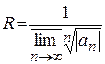 . Будем считать, что если
. Будем считать, что если  , то
, то  , а если
, а если 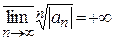 , то
, то  .
.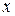 , удовлетворяющих условию
, удовлетворяющих условию  . Если
. Если 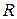 конечное число, то он расходится
конечное число, то он расходится  .
. – конечный, и выполняется неравенство
– конечный, и выполняется неравенство  , тогда
, тогда .
.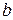 такое, что
такое, что .
. может не выполниться лишь для конечного числа номеров
может не выполниться лишь для конечного числа номеров  . Поэтому существует такой номер
. Поэтому существует такой номер  , что
, что  выполняется
выполняется ,
, , при
, при  . (11)
. (11) сходится, как геометрическая прогрессия
сходится, как геометрическая прогрессия  , то ряд
, то ряд  тоже сходится, по признаку Вейерштарсса.
тоже сходится, по признаку Вейерштарсса. , тогда
, тогда  и получаем
и получаем  . Выберем число
. Выберем число 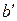 , такое, чтобы
, такое, чтобы . (12)
. (12) сходящаяся к
сходящаяся к 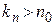 выполняется
выполняется  . Откуда
. Откуда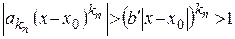
 при
при 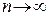 , т.е. нарушено необходимое условие сходимости ряда. ■
, т.е. нарушено необходимое условие сходимости ряда. ■ (13)
(13) ряд сходится только в одной точке
ряд сходится только в одной точке  ряд сходится в интервале
ряд сходится в интервале  , а при
, а при  ряд сходится для
ряд сходится для  . Таким образом, областью сходимости степенного ряда является интервал. В граничных точках
. Таким образом, областью сходимости степенного ряда является интервал. В граничных точках  и
и  ряд может и сходится и расходится, поэтому требуется дополнительное исследование. Формулу (13) используют для нахождения радиуса сходимости степенного ряда. Для определения интервала сходимости на практике часто также удобно использовать признак Даламбера для ряда составленного из модулей членов исходного степенного ряда.
ряд может и сходится и расходится, поэтому требуется дополнительное исследование. Формулу (13) используют для нахождения радиуса сходимости степенного ряда. Для определения интервала сходимости на практике часто также удобно использовать признак Даламбера для ряда составленного из модулей членов исходного степенного ряда. .
.
 ,
, .
. , то
, то 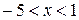 . Таким образом, интервал сходимости ряда
. Таким образом, интервал сходимости ряда  используем сходимость на концах интервала. При
используем сходимость на концах интервала. При  получаем числовой ряд
получаем числовой ряд  , а при
, а при 
 оба ряда сходятся, причем первый сходится абсолютно, как обобщенный гармонический ряд.
оба ряда сходятся, причем первый сходится абсолютно, как обобщенный гармонический ряд.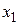 , то он абсолютно сходится для
, то он абсолютно сходится для  .
.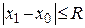 . Это так, потому что, если
. Это так, потому что, если  , то по теореме 8 степенной ряд расходится в точке
, то по теореме 8 степенной ряд расходится в точке  . <
. < , содержащимся в интервале сходимости.
, содержащимся в интервале сходимости. , т.е. числовой ряд
, т.е. числовой ряд  – сходится.
– сходится. выполняется
выполняется  , но так как
, но так как  – сходится, то по признаку Вейерштрасса равномерно сходится ряд (10) на
– сходится, то по признаку Вейерштрасса равномерно сходится ряд (10) на  , (14)
, (14)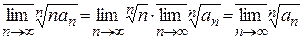 .
. . По теореме 10 ряд сходится равномерно на
. По теореме 10 ряд сходится равномерно на  .
. , при
, при 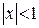 .
. ,
,  в степенной ряд.
в степенной ряд.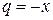
 .
.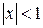
 .
. .
.


