Глава 12. Функциональные ряды
Пусть 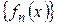 последовательность функций, каждая из которых определена на некотором подмножестве
последовательность функций, каждая из которых определена на некотором подмножестве 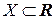 . В этом случае говорят, что на множестве
. В этом случае говорят, что на множестве  задана функциональная последовательность
задана функциональная последовательность 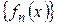 . Например:
. Например:
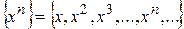 ,
,
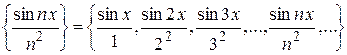 .
.
Аналогично, если задан ряд 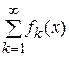 , каждый член которого является функцией, определенной на множестве
, каждый член которого является функцией, определенной на множестве  , то говорят, что на множестве
, то говорят, что на множестве  задан функциональный ряд. Например,
задан функциональный ряд. Например, 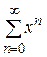 ,
, 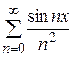 .
.
Определение 1. Функциональная последовательность 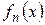 называется схдящейся на множестве
называется схдящейся на множестве  к функции
к функции 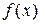 , если
, если 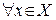 последовательность
последовательность 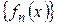 сходится к
сходится к 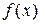 , т.е.
, т.е. 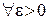
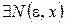 такое, что выполняется
такое, что выполняется  для
для 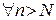 .
.
Обозначается 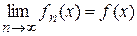 . Эта сходимость называется монотонной, т.е. сходимостью в каждой точке множества.
. Эта сходимость называется монотонной, т.е. сходимостью в каждой точке множества.
Определение 2. Функциональный ряд 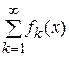 называется сходящимся намножестве
называется сходящимся намножестве  к функции
к функции 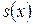 , если последовательность его частных сумм
, если последовательность его частных сумм 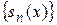 сходится к функции
сходится к функции 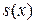 на множестве
на множестве  , которое называется областью сходимости ряда.
, которое называется областью сходимости ряда.
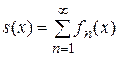 ,
, 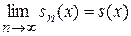 .
.
Функция 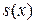 называется суммой функционального ряда.
называется суммой функционального ряда.
Один из основных вопросов, рассматриваемых в теории функциональных рядов – нахождение области сходимости функционального ряда.
Пример 1. Найти область сходимости следующих рядов:
а) 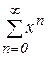 ; б)
; б) 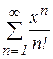 ; в)
; в) 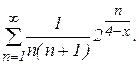
Решение. а) 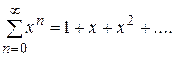 – бесконечная геометрическая про- грессия. На множестве X=(-1,1) ряд сходится, причем
– бесконечная геометрическая про- грессия. На множестве X=(-1,1) ряд сходится, причем 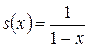 .
.
б ) По признаку Даламбера ряд 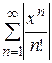 сходится для
сходится для 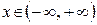 . Следовательно, исходный ряд сходится абсолютно для
. Следовательно, исходный ряд сходится абсолютно для 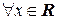 .
.
в) По признаку Коши 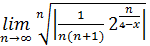 =
= 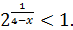 Откуда следует, что х>4. Областью сходимости является множество X=(4,+
Откуда следует, что х>4. Областью сходимости является множество X=(4,+ 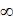 ).
).
Кроме поточечной сходимости 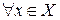 , есть также другой тип сходисти, которая называется равномерной сходимостью на множестве.
, есть также другой тип сходисти, которая называется равномерной сходимостью на множестве.
Определение 3. Последовательность 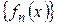 называется равномерно сходящейся на множестве
называется равномерно сходящейся на множестве  к функции
к функции 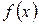 , если
, если 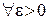
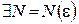 такое, что
такое, что 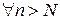 и
и 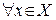 выполняется
выполняется  . Обозначается
. Обозначается 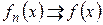 .
.
Определение 4. Функциональный ряд 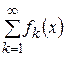 называется равномерно сходящимся на множестве
называется равномерно сходящимся на множестве  к функции
к функции 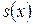 , если последовательность его частичных сумм
, если последовательность его частичных сумм  сходится равномерно на
сходится равномерно на  к
к 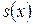 .
.
Сравним между собой оба типа сходимости. Пусть ряд 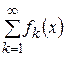 сходит- ся для
сходит- ся для 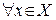 . Это означает, что каждому
. Это означает, что каждому 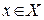 будет соответствовать свой числовой ряд, для сходимости которого
будет соответствовать свой числовой ряд, для сходимости которого 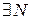 , определенное в каждой точке. В общем случае значение
, определенное в каждой точке. В общем случае значение 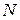 будет меняться от точки к точке, т.е.
будет меняться от точки к точке, т.е. 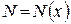 . При равномерной сходимости требуется, чтобы для выбранного
. При равномерной сходимости требуется, чтобы для выбранного 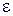 число
число 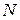 не зависело от
не зависело от 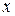 и было одним и тем же для
и было одним и тем же для 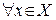 .
.
Отсюда следует важный вывод: если последовательность (ряд) равномер но сходится на  , то последовательность (ряд) просто сходятся на
, то последовательность (ряд) просто сходятся на  . Обратное утверждение неверно.
. Обратное утверждение неверно.
Пример 2. Проверить сходимость последовательности 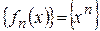 ,
, 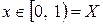 .
.
Решение. Понятно, что 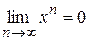 , т.е. последовательность сходится. Однако эта сходимость будет неравномерной. Действительно, возьмем
, т.е. последовательность сходится. Однако эта сходимость будет неравномерной. Действительно, возьмем  . Найдется ли
. Найдется ли 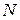 такое, что для
такое, что для 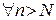 и
и 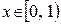 выполняется неравенство
выполняется неравенство 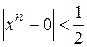 ? Выполнение этого неравенства для всех точек
? Выполнение этого неравенства для всех точек 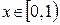 невозможно, так как при х близких к 1
невозможно, так как при х близких к 1 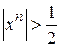 , потому что
, потому что  . Таким образом, последовательность сходится, но неравномерно.
. Таким образом, последовательность сходится, но неравномерно.
Пример 3. Рассмотрим ряд 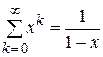 . Он сходится на
. Он сходится на 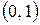 . Покажем, что он сходится неравномерно.
. Покажем, что он сходится неравномерно.
Решение. Последовательность частичных сумм 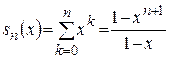 сходится к
сходится к 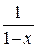 при
при 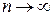 . Поэтому для
. Поэтому для 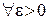
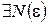 такое, что
такое, что 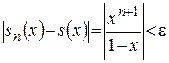 для
для 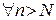 . Однако для
. Однако для 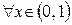 это невозможно, так как при
это невозможно, так как при 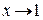 функция
функция 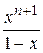 принимает любое, как угодно большое значение. Ряд сходится, но неравномерно.
принимает любое, как угодно большое значение. Ряд сходится, но неравномерно.
Теорема 1. (критерий Коши). а) Для того, чтобы последовательность 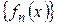 равномерно сходилась на множестве
равномерно сходилась на множестве  необходимо и достаточно, чтобы для
необходимо и достаточно, чтобы для 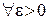
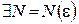 таких, что для
таких, что для 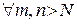 и
и 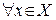 выполнялось
выполнялось
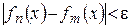 ; (1)
; (1)
б) Для того, чтобы функциональный ряд 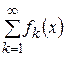 равномерно сходился на множестве
равномерно сходился на множестве  , необходимо и достаточно, чтобы для
, необходимо и достаточно, чтобы для 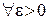
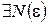 таких, что для
таких, что для 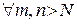 и
и 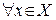 выполнялось
выполнялось 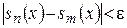 , или, если обозначить
, или, если обозначить 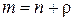 , то
, то
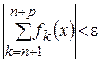 ,
, 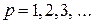 (2)
(2)
Доказательство выполним для последовательностей.
‰ Необходимость. Пусть 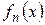 равномерно сходится к
равномерно сходится к 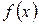 на
на  . Зададим
. Зададим 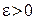 , тогда
, тогда  , что
, что 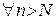 и
и 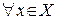
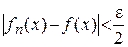 .
.
Возьмем 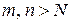 , тогда для
, тогда для 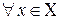 имеем
имеем
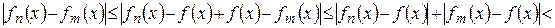
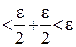 , т.е. выполняется (1).
, т.е. выполняется (1).
Достаточность. Пусть выполняется условие теоремы а), т.е. для 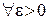
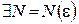 такие, что для
такие, что для 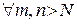 и
и 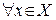 выполняется
выполняется 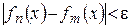 . Это означает, что для
. Это означает, что для 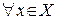 числовая последовательность
числовая последовательность 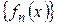 фундаментальная, а, следовательно, она сходится. Положим
фундаментальная, а, следовательно, она сходится. Положим 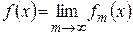 . Перейдем к пределу в неравенстве
. Перейдем к пределу в неравенстве 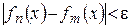 при
при 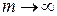 . Тогда получим, что для
. Тогда получим, что для 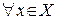 выполняется неравенство
выполняется неравенство 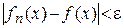 , т.е.
, т.е. 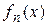 сходится равномерно к
сходится равномерно к 
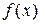 на
на  , при
, при 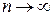 . <
. <
Пример 4. Исследовать сходимость ряда 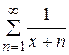 на интервале
на интервале 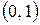 .
.
Решение. Неравенство 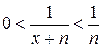 ,
, 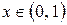 ,
, 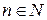 показывает, что последовательность
показывает, что последовательность 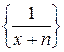 сходится к нулю равномерно на
сходится к нулю равномерно на 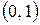 , но в тоже время для любого значения
, но в тоже время для любого значения 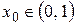 ряд
ряд  расходится.
расходится.
Теорема 2. (Признак Вейерштрасса). Пусть для 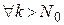 и
и 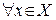 выполняются неравенства
выполняются неравенства 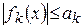 и числовой ряд
и числовой ряд 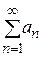 сходится. Тогда функциональный ряд
сходится. Тогда функциональный ряд 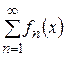 сходится абсолютно и равномерно на множестве
сходится абсолютно и равномерно на множестве  .
.
‰ Так как числовой ряд 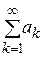 сходится, то для него выполняется критерий Коши, т.е.
сходится, то для него выполняется критерий Коши, т.е. 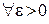
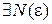 , что выполняется
, что выполняется 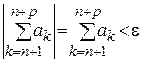 для
для 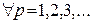
Возьмем 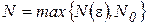 и
и 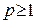 , тогда для
, тогда для 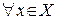 имеем
имеем
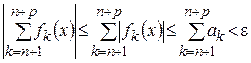 ,
, 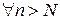 ,
,
т.е. выполняется критерий Коши (2). Ряд сходится равномерно и абсолютно по признаку сравнения. ■
Замечание. Ряд 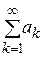 в теореме 2 называется мажорантой для ряда
в теореме 2 называется мажорантой для ряда  , а саму теорему 2 часто называют мажорантным признаком сходимости.
, а саму теорему 2 часто называют мажорантным признаком сходимости.
Пример 5. Доказать сходимость ряда 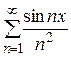 .
.
Решение. Рассмотрим ряд 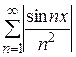 . Этот ряд сходится абсолютно, т.к. по признаку сравнения
. Этот ряд сходится абсолютно, т.к. по признаку сравнения 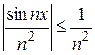 . Поэтому исходный ряд абсолютно и равномерно сходится
. Поэтому исходный ряд абсолютно и равномерно сходится 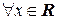 .
.
Пример 6. Исследовать сходимость ряда 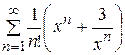 на отрезке
на отрезке 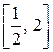 .
.
Решение. Первое слагаемое в сумме 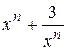 принимает наибольшее значение в точке
принимает наибольшее значение в точке 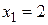 , второе в точке
, второе в точке 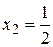 . Следовательно, для всех
. Следовательно, для всех 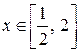 имеем, что
имеем, что 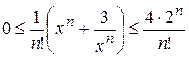 , и в силу признака Вейерштрасса получаем, что данный ряд сходится равномерно на
, и в силу признака Вейерштрасса получаем, что данный ряд сходится равномерно на  .
.
Признак Вейерштрасса дает только достаточное условие. Непосредственно из определения вытекает необходимый и достаточный признак равномерной сходимости, которым удобно пользоваться на практике.
Теорема 3. Для того чтобы функциональная последовательность 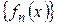 равномерно сходилась на множестве
равномерно сходилась на множестве  к предельной функции
к предельной функции 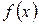 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы
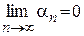 , (3)
, (3)
где 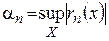 ,
, 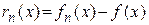 .
.
‰ Необходимость. Пусть 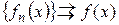 при
при 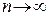 . Так как по определению
. Так как по определению 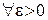 неравенство
неравенство  выполняется для
выполняется для 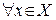 и при
и при 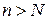 , то при таких
, то при таких  будет справедливо
будет справедливо 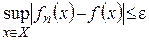 . Отсюда следует, что
. Отсюда следует, что 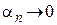 при
при 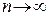 .
.
Достаточность. Пусть 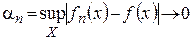 при
при 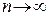 . Это означает, что для
. Это означает, что для 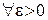 при достаточно больших
при достаточно больших 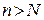 будет выполняться
будет выполняться 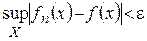 , тогда тем более для всех
, тогда тем более для всех 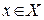 и
и 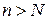 будет выполняться
будет выполняться 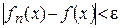 . А это означает равномерную сходимость. <
. А это означает равномерную сходимость. <
Теперь, пользуясь этой теоремой и определением равномерно сходящегося функционального ряда, можно сформулировать необходимое и достаточное условия равномерной сходимости ряда: для того, чтобы функциональный ряд 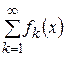 сходился к
сходился к 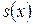 на
на  необходимо и достаточно, чтобы функциональная последовательность
необходимо и достаточно, чтобы функциональная последовательность 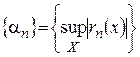 равномерно сходилась к нулю, т.е.
равномерно сходилась к нулю, т.е. 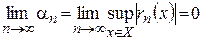 .
.
Пример 7. Исследовать сходимость 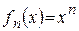
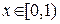 .
.
Решение. Ранее было показано, что сходимость есть, но она неравномерная. Это же самое получается более просто по теореме 3:
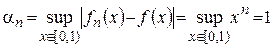 .
.
При этом 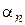 не стремится к 0 при
не стремится к 0 при 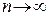 , поэтому сходимость неравномерная.
, поэтому сходимость неравномерная.
Пример 8. Сходится ли равномерно последовательность 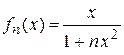 ,
, 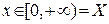 .
.
Решение. Сначала проверим существование предельной функции 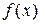 .
.
 при
при 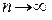 ,
, 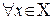 .
.
Таким образом, 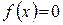 . Рассмотрим
. Рассмотрим
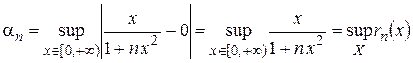 ,
,
где 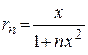 .
.
Найдем 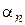 , т.е. наибольшее значение
, т.е. наибольшее значение 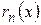 на
на  . Вычислим значения
. Вычислим значения 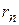 на концах интервала
на концах интервала
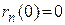 и
и 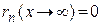
и в критических точках. Продифференцируем 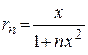 :
:
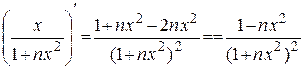 .
.
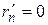 при
при 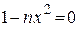 , откуда
, откуда 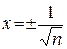 .
.
При этом берем только 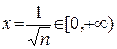 . Тогда
. Тогда 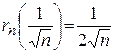 . Поэтому
. Поэтому 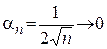 при
при 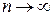 . Следовательно,
. Следовательно, 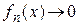 при
при 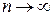 на
на 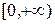 . Последовательность
. Последовательность 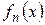 равномерно сходится на
равномерно сходится на 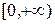 .
.
Пример 9. Проверить сходимость ряда 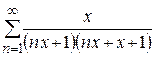 ,
, 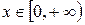 .
.
Решение. Прежде всего, отметим, что в указанном промежутке ряд сходится по признаку сравнения, так как он знакоположительный, и существует сходящийся ряд 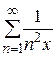 для
для 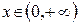 , так что выполняется условие
, так что выполняется условие 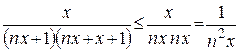 .
.
Рассмотрим остаток 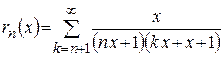 и найдем его сумму. Так как
и найдем его сумму. Так как 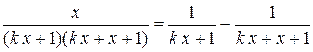 , то т -я частичная сумма остатка
, то т -я частичная сумма остатка 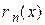 будет
будет
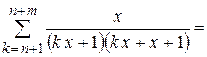
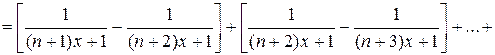
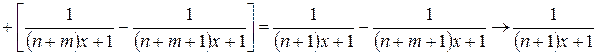 , при
, при 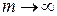 .
.
Т.е. 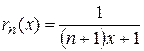 . Тогда
. Тогда 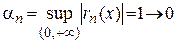 при
при 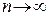 . Таким образом, на
. Таким образом, на 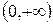 ряд сходится неравномерно. На любом промежутке
ряд сходится неравномерно. На любом промежутке 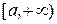 , где
, где 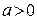 сходимость равномерная, т.к.
сходимость равномерная, т.к.
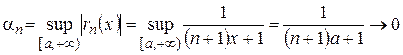 при
при 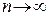 .
.
Пример 10. Исследовать на равномерную сходимость ряд 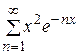 на
на 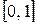 .
.
Решение. Так как 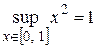 ,
, 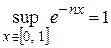 , то оценка
, то оценка 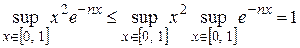 не дает сходящегося мажорантного ряда. Найдем
не дает сходящегося мажорантного ряда. Найдем 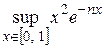 . Поскольку
. Поскольку 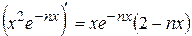 , то
, то 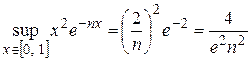 , следовательно,
, следовательно,  ,
, 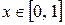 и в силу признака Вейерштрасса ряд сходится равномерно на
и в силу признака Вейерштрасса ряд сходится равномерно на 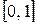 .
.

 последовательность функций, каждая из которых определена на некотором подмножестве
последовательность функций, каждая из которых определена на некотором подмножестве 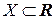 . В этом случае говорят, что на множестве
. В этом случае говорят, что на множестве  задана функциональная последовательность
задана функциональная последовательность 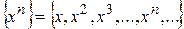 ,
,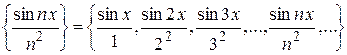 .
.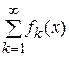 , каждый член которого является функцией, определенной на множестве
, каждый член которого является функцией, определенной на множестве 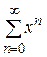 ,
, 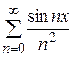 .
.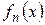 называется схдящейся на множестве
называется схдящейся на множестве  , если
, если 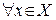 последовательность
последовательность 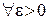
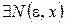 такое, что выполняется
такое, что выполняется  для
для 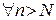 .
.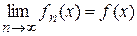 . Эта сходимость называется монотонной, т.е. сходимостью в каждой точке множества.
. Эта сходимость называется монотонной, т.е. сходимостью в каждой точке множества.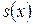 , если последовательность его частных сумм
, если последовательность его частных сумм 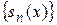 сходится к функции
сходится к функции 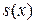 на множестве
на множестве 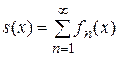 ,
, 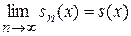 .
.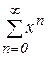 ; б)
; б) 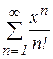 ; в)
; в) 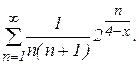
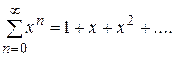 – бесконечная геометрическая про- грессия. На множестве X=(-1,1) ряд сходится, причем
– бесконечная геометрическая про- грессия. На множестве X=(-1,1) ряд сходится, причем 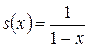 .
.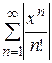 сходится для
сходится для 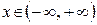 . Следовательно, исходный ряд сходится абсолютно для
. Следовательно, исходный ряд сходится абсолютно для 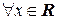 .
.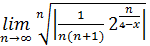 =
= 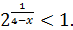 Откуда следует, что х>4. Областью сходимости является множество X=(4,+
Откуда следует, что х>4. Областью сходимости является множество X=(4,+ 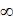 ).
).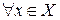 , есть также другой тип сходисти, которая называется равномерной сходимостью на множестве.
, есть также другой тип сходисти, которая называется равномерной сходимостью на множестве.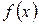 , если
, если 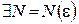 такое, что
такое, что 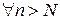 и
и 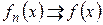 .
.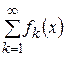 называется равномерно сходящимся на множестве
называется равномерно сходящимся на множестве  сходится равномерно на
сходится равномерно на 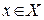 будет соответствовать свой числовой ряд, для сходимости которого
будет соответствовать свой числовой ряд, для сходимости которого 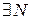 , определенное в каждой точке. В общем случае значение
, определенное в каждой точке. В общем случае значение 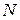 будет меняться от точки к точке, т.е.
будет меняться от точки к точке, т.е. 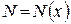 . При равномерной сходимости требуется, чтобы для выбранного
. При равномерной сходимости требуется, чтобы для выбранного 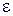 число
число 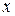 и было одним и тем же для
и было одним и тем же для 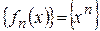 ,
, 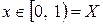 .
.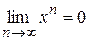 , т.е. последовательность сходится. Однако эта сходимость будет неравномерной. Действительно, возьмем
, т.е. последовательность сходится. Однако эта сходимость будет неравномерной. Действительно, возьмем  . Найдется ли
. Найдется ли 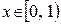 выполняется неравенство
выполняется неравенство 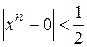 ? Выполнение этого неравенства для всех точек
? Выполнение этого неравенства для всех точек 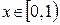 невозможно, так как при х близких к 1
невозможно, так как при х близких к 1 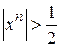 , потому что
, потому что  . Таким образом, последовательность сходится, но неравномерно.
. Таким образом, последовательность сходится, но неравномерно.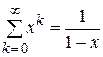 . Он сходится на
. Он сходится на  . Покажем, что он сходится неравномерно.
. Покажем, что он сходится неравномерно.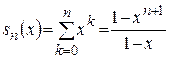 сходится к
сходится к 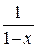 при
при 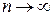 . Поэтому для
. Поэтому для 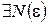 такое, что
такое, что 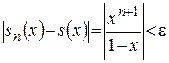 для
для 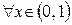 это невозможно, так как при
это невозможно, так как при 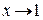 функция
функция 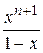 принимает любое, как угодно большое значение. Ряд сходится, но неравномерно.
принимает любое, как угодно большое значение. Ряд сходится, но неравномерно.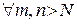 и
и 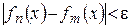 ; (1)
; (1)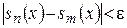 , или, если обозначить
, или, если обозначить 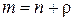 , то
, то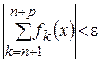 ,
, 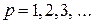 (2)
(2)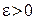 , тогда
, тогда  , что
, что 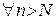 и
и 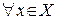
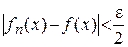 .
.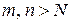 , тогда для
, тогда для 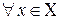 имеем
имеем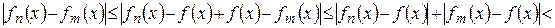
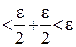 , т.е. выполняется (1).
, т.е. выполняется (1).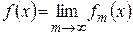 . Перейдем к пределу в неравенстве
. Перейдем к пределу в неравенстве 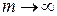 . Тогда получим, что для
. Тогда получим, что для 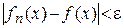 , т.е.
, т.е. 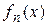 сходится равномерно к
сходится равномерно к 
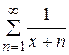 на интервале
на интервале 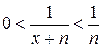 ,
, 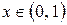 ,
, 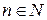 показывает, что последовательность
показывает, что последовательность 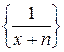 сходится к нулю равномерно на
сходится к нулю равномерно на 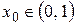 ряд
ряд  расходится.
расходится.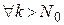 и
и 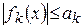 и числовой ряд
и числовой ряд 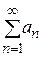 сходится. Тогда функциональный ряд
сходится. Тогда функциональный ряд 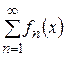 сходится абсолютно и равномерно на множестве
сходится абсолютно и равномерно на множестве 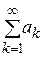 сходится, то для него выполняется критерий Коши, т.е.
сходится, то для него выполняется критерий Коши, т.е. 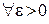
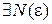 , что выполняется
, что выполняется 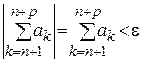 для
для 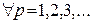
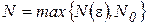 и
и 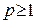 , тогда для
, тогда для 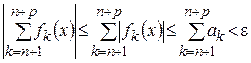 ,
,  , а саму теорему 2 часто называют мажорантным признаком сходимости.
, а саму теорему 2 часто называют мажорантным признаком сходимости.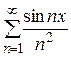 .
.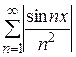 . Этот ряд сходится абсолютно, т.к. по признаку сравнения
. Этот ряд сходится абсолютно, т.к. по признаку сравнения 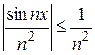 . Поэтому исходный ряд абсолютно и равномерно сходится
. Поэтому исходный ряд абсолютно и равномерно сходится 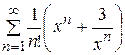 на отрезке
на отрезке  .
.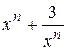 принимает наибольшее значение в точке
принимает наибольшее значение в точке 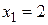 , второе в точке
, второе в точке 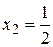 . Следовательно, для всех
. Следовательно, для всех 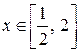 имеем, что
имеем, что 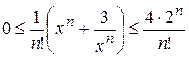 , и в силу признака Вейерштрасса получаем, что данный ряд сходится равномерно на
, и в силу признака Вейерштрасса получаем, что данный ряд сходится равномерно на 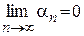 , (3)
, (3)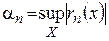 ,
, 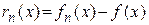 .
.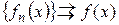 при
при 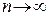 . Так как по определению
. Так как по определению 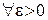 неравенство
неравенство 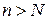 , то при таких
, то при таких  будет справедливо
будет справедливо 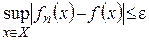 . Отсюда следует, что
. Отсюда следует, что 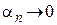 при
при 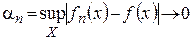 при
при 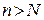 будет выполняться
будет выполняться 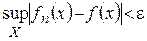 , тогда тем более для всех
, тогда тем более для всех 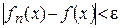 . А это означает равномерную сходимость. <
. А это означает равномерную сходимость. <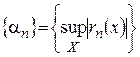 равномерно сходилась к нулю, т.е.
равномерно сходилась к нулю, т.е. 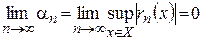 .
.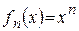
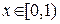 .
.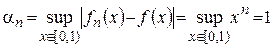 .
.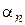 не стремится к 0 при
не стремится к 0 при 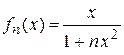 ,
, 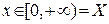 .
. при
при 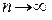 ,
, 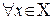 .
.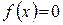 . Рассмотрим
. Рассмотрим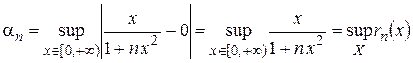 ,
,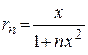 .
.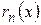 на
на 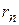 на концах интервала
на концах интервала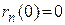 и
и 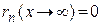
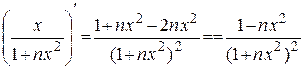 .
.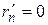 при
при 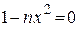 , откуда
, откуда 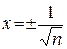 .
.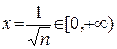 . Тогда
. Тогда 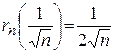 . Поэтому
. Поэтому 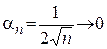 при
при 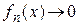 при
при 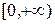 . Последовательность
. Последовательность 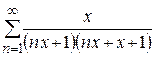 ,
, 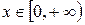 .
.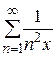 для
для 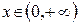 , так что выполняется условие
, так что выполняется условие 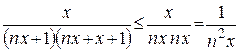 .
.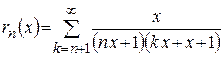 и найдем его сумму. Так как
и найдем его сумму. Так как 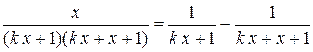 , то т -я частичная сумма остатка
, то т -я частичная сумма остатка 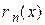 будет
будет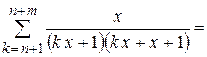
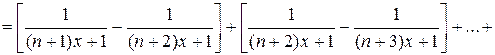
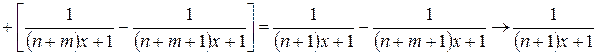 , при
, при 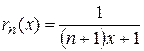 . Тогда
. Тогда 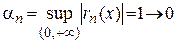 при
при 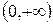 ряд сходится неравномерно. На любом промежутке
ряд сходится неравномерно. На любом промежутке 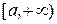 , где
, где 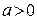 сходимость равномерная, т.к.
сходимость равномерная, т.к.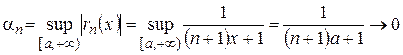 при
при 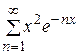 на
на 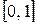 .
.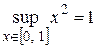 ,
, 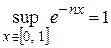 , то оценка
, то оценка 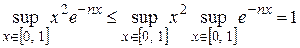 не дает сходящегося мажорантного ряда. Найдем
не дает сходящегося мажорантного ряда. Найдем 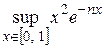 . Поскольку
. Поскольку 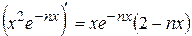 , то
, то 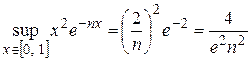 , следовательно,
, следовательно,  ,
, 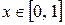 и в силу признака Вейерштрасса ряд сходится равномерно на
и в силу признака Вейерштрасса ряд сходится равномерно на 


