Тригонометрические ряды Фурье
Функциональная последовательность
называется основной тригонометрической системой (ОТС). Функциональная последовательность
где Лемма. Основная тригонометрическая система ортогональна на отрезке
Тригонометрическая система общего вида ортогональна на
‰ Справедливость этих равенств устанавливается непосредственным интегрированием, применением формул
Ясно, что по функциональной последовательности, состоящей их основной тригонометрической системы, можно построить функциональный ряд вида
Этот ряд называется тригонометрическим рядом по ОТС. Функциональный ряд по тригонометрической системе общего вида следующий
Каждое слагаемое тригонометрического ряда называется гармоническимколебанием или гармоникой, и его можно записать в виде
где Любая частичная сумма ряда имеет период Если Теорема 14. Если тригонометрический ряд (20) равномерно сходится на всей числовой прямой к функции
тогда коэффициенты этого ряда определяются по формулам
‰ Для доказательства используем лемму. Умножим (22) на 1 и проинтегрируем на отрезке Аналогичная теорема имеет место для равномерно сходящегося тригометрического ряда по тригонометрической системе общего вида. Если
то
Дальше все рассуждения будут проводиться для ряда (20), т.к заменой Определение 6. Если функция Пример 24. Решение. Найдем коэффициенты ряда по формулам (23). Используя формулу интегрирования по частям, получим:
В теории рядов Фурье особое значение имеет вопрос: если
|


 ,
,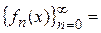
 ,
,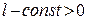 , называется тригонометрической системой общего вида.
, называется тригонометрической системой общего вида. , т.е. выполняются следующие равенства:
, т.е. выполняются следующие равенства: ,
,  ,
,  ,
,  ,
,  , при
, при  .
. ,
,  ,
,  при
при  .
. , т.е.
, т.е.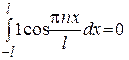 ;
;  ;
;  ;
;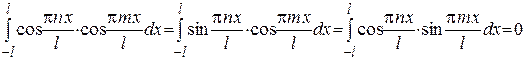 , при
, при  ,
,  , при
, при 
 ,
,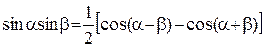 ,
, ,
, ,
, .
.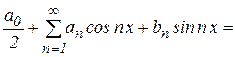 (20)
(20) 
 (21)
(21) ,
, – амплитуда,
– амплитуда,  – частота,
– частота,  – начальная фаза.
– начальная фаза. , т.к. входящие в нее функции имеют период
, т.к. входящие в нее функции имеют период  , то он сходится на всей числовой прямой. Его сумма, будучи пределом последовательности периодических частичных сумм, также является периодической функцией с периодом
, то он сходится на всей числовой прямой. Его сумма, будучи пределом последовательности периодических частичных сумм, также является периодической функцией с периодом  сумма ряда (20) на некотором множестве
сумма ряда (20) на некотором множестве  , то можно выразить коэффициенты ряда
, то можно выразить коэффициенты ряда  и
и  через
через  ,
,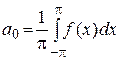 ,
, 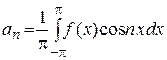 ,
,  (22)
(22) , на
, на  и проинтегрируем,
и проинтегрируем, 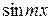 и проинтегрируем на отрезке
и проинтегрируем на отрезке  ,
, ,
,  ,
,  . (23)
. (23) , ряд (21) сводится к ряду (20)
, ряд (21) сводится к ряду (20) абсолютно интегрируема на
абсолютно интегрируема на  ,
,  . Найти коэффициенты Фурье и составить ряд Фурье.
. Найти коэффициенты Фурье и составить ряд Фурье. ,
,  ,
,  .
. .
. это возможно? Ответы на это вопросы будут даны ниже.
это возможно? Ответы на это вопросы будут даны ниже.


