Теорема 4. (о перестановочности предельного перехода и суммирования).
а) Пусть выполняются условия:
1) последовательность 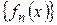 равномерно сходится к функции
равномерно сходится к функции 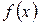 на множестве
на множестве 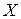 ;
;
2)  – предельная точка множества
– предельная точка множества 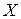 ;
;
3) 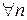 существуют пределы
существуют пределы 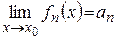 .
.
Тогда последовательность 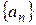 сходится и
сходится и
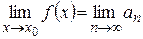 . (4)
. (4)
б) Пусть выполняются условия:
1) ряд 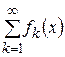 равномерно сходится к
равномерно сходится к 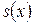 на
на 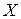 ;
;
2)  – предельная точка множества
– предельная точка множества 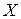 ;
;
3) существуют пределы 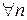
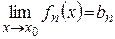 .
.
Тогда ряд 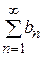 – сходится, причем
– сходится, причем
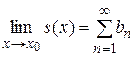 . (5)
. (5)
‰ Доказательство выполним только для последовательности. Покажем, что последовательность 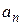 сходится. Т.к.
сходится. Т.к.  сходится равномерно на
сходится равномерно на 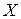 , то в силу критерия Коши (теорема 1) для
, то в силу критерия Коши (теорема 1) для 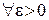
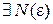 такие, что
такие, что  и
и 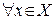 выполняется
выполняется 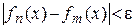 . Переходя к пределу в неравенстве при
. Переходя к пределу в неравенстве при  , так как
, так как 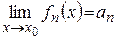 , получим
, получим 
 , т.е. последовательность фундаментальная, а это означает, что она сходится.
, т.е. последовательность фундаментальная, а это означает, что она сходится.
Докажем справедливость формулы (4). Возьмем 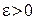 . В силу равномерной сходимости
. В силу равномерной сходимости 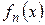 для
для 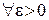
 такое, что
такое, что 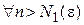 и
и 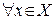 выполняется
выполняется
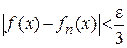 . (6)
. (6)
Так как 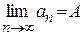 , то для
, то для 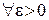
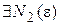 выполняется
выполняется
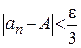 . (7)
. (7)
Возьмем  . Для этого N справедливы неравенства (6) и (7). Так как
. Для этого N справедливы неравенства (6) и (7). Так как 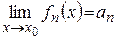 , то
, то  , что выполнится
, что выполнится
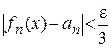 при
при 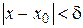 . (8)
. (8)
Тогда 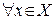
 будем иметь из (6) – (8):
будем иметь из (6) – (8):
 ,
,
т.е. 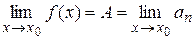 <
<
Замечание. Поскольку 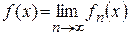 ,
, 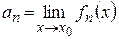 , то (4) можно записать
, то (4) можно записать
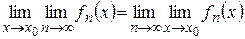 .
.
Таким образом, в случае равномерной сходимости и при существовании  , порядок взятия предела можно изменять.
, порядок взятия предела можно изменять.
Аналогично для функциональных рядов имеем
 .
.
Таким образом, если ряд равномерно сходится на множестве  и существуют пределы
и существуют пределы 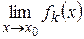 , то операции предельного перехода и суммирования перестановочны.
, то операции предельного перехода и суммирования перестановочны.
Теорема 5. (о непрерывности предельной функции и суммы ряда).
а) Пусть последовательность 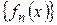 непрерывных на отрезке
непрерывных на отрезке 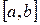 функций равномерно сходится к
функций равномерно сходится к 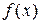 на
на 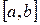 , тогда ее предел
, тогда ее предел 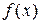 также непрерывная на [ a, b ] функция.
также непрерывная на [ a, b ] функция.
б) Пусть все члены ряда 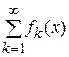 непрерывные на
непрерывные на 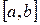 функции, а сам ряд сходится равномерно на
функции, а сам ряд сходится равномерно на 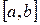 , тогда его сумма
, тогда его сумма 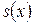 также непрерывна на
также непрерывна на 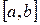
‰ Доказательство для рядов. Пусть 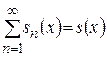 . Надо доказать, что
. Надо доказать, что 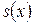 непрерывна для
непрерывна для 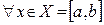 . Возьмем
. Возьмем 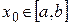 и найдем предел
и найдем предел 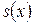 в этой точке. Используя предыдущую теорему, получим
в этой точке. Используя предыдущую теорему, получим
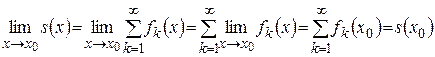 .
.
Аналогично для последовательности. <
Если последовательность непрерывных функций (ряд) сходится неравномерно, то ее предел (сумма ряда) может быть разрывной функцией.
Пример 11. 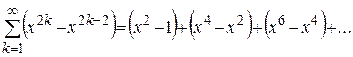 на отрезке
на отрезке 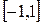 .
.
Решение. Члены ряда 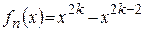 непрерывны на
непрерывны на 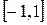 и
и 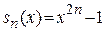 .
.
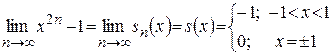 ,
,
т.е. получили, что 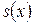 – разрывная в точках
– разрывная в точках  .
.
Теорема 6. (о дифференцировании функциональных последовательностей и рядов).
а) Пусть задана последовательность 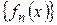 , удовлетворяющая следующим условиям:
, удовлетворяющая следующим условиям:
1) 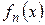 дифференцируема на
дифференцируема на 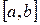 для
для 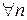 ;
;
2) последовательность 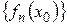 сходится при некотором
сходится при некотором 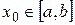 ;
;
3) последовательность 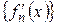 равномерно сходится на
равномерно сходится на 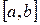 .
.
Тогда последовательность 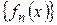 равномерно сходится на отрезке
равномерно сходится на отрезке 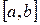 к некоторой функции
к некоторой функции 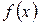 и (
и ( ), причем
), причем
 ,
,  . (9)
. (9)
б) Пусть ряд 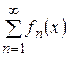 удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
1) 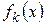 для
для 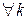 дифференцируема на
дифференцируема на 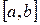 ;
;
2) ряд 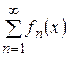 сходится при некотором
сходится при некотором 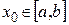 ;
;
3) ряд 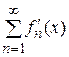 сходится равномерно на
сходится равномерно на 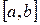 .
.
Тогда ряд 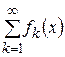 сходится равномерно на
сходится равномерно на 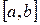 к некоторой функции
к некоторой функции 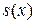 , т.е.
, т.е. 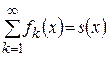 , и причем
, и причем
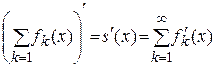 .
.
‰ Доказательство приведем для последовательности. Покажем, что 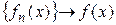 и сходится равномерно на
и сходится равномерно на 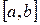 . Используем критерий Коши. Пусть
. Используем критерий Коши. Пусть 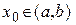 и
и 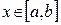 . Из очевидного тождества
. Из очевидного тождества
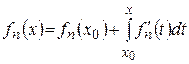 для
для 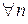
получим следующее неравенство
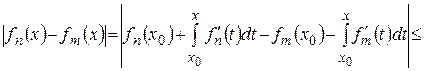
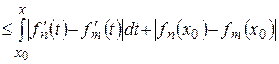 ,
,  .
.
Возьмем произвольное 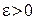 . Т.к. последовательность
. Т.к. последовательность 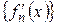 сходится равномерно на
сходится равномерно на 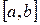 , то
, то 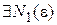 , что при всех
, что при всех 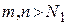 и для
и для 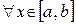 выполнится
выполнится
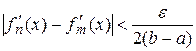 .
.
Так как 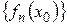 сходится, то
сходится, то 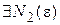 , что для
, что для  выполняется
выполняется
 .
.
Тогда получаем
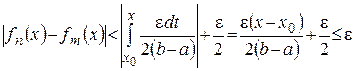
для 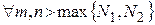 и
и  , следовательно, в силу критерия Коши, последовательность
, следовательно, в силу критерия Коши, последовательность 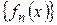 равномерно сходится на
равномерно сходится на 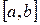 к
к 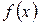 .
.
Докажем равенство (9). Пусть 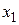 – произвольная точка
– произвольная точка 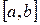 . Рассмотрим последовательность
. Рассмотрим последовательность  определенную на множестве
определенную на множестве  и докажем, что она сходится равномерно. Рассмотрим
и докажем, что она сходится равномерно. Рассмотрим  . Применим к
. Применим к 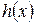 формулу Лагранжа
формулу Лагранжа 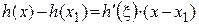
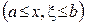 или
или
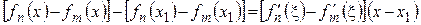 .
.
Тогда
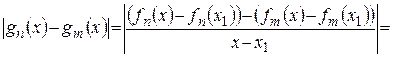
 ,
,
т.к. последовательность 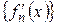 сходится равномерно.
сходится равномерно.
Таким образом, для 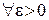
 , что выполняется
, что выполняется  для
для  и
и  в силу равномерной сходимости
в силу равномерной сходимости  . Откуда следует, что последовательность
. Откуда следует, что последовательность 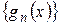 сходится равномерно на
сходится равномерно на 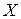 , причем
, причем
 .
.
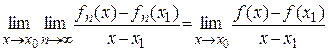 .
.
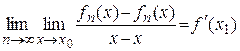 .
.
Поэтому 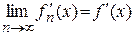 , и по определению производной выполняется
, и по определению производной выполняется 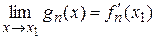 .
.
Тогда по теореме 1 последовательность 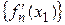 сходится, причем
сходится, причем 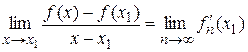 . Так как
. Так как 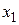 произвольная точка
произвольная точка 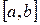 , то теорема доказана. <
, то теорема доказана. <
Таким образом, при выполнении условий теоремы операции предельного перехода и дифференцирования, а также суммирование и дифференцирование перестановочны.
Отметим, что если в теореме отбросить условие равномерной сходимости  на
на 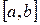 , то теорема неверна.
, то теорема неверна.
Теорема 7. (об интегрировании функциональных последовательностей и рядов).
а) Пусть последовательность 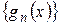 равномерно сходится к некоторой функции
равномерно сходится к некоторой функции  на отрезке
на отрезке 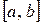 , причем каждая
, причем каждая 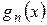 имеет первообразную на
имеет первообразную на 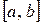 . Тогда
. Тогда
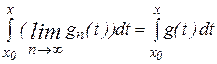 .
.
б) Пусть ряд 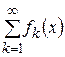 равномерно сходится на отрезке
равномерно сходится на отрезке 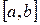 , причем каждая из функций
, причем каждая из функций 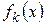 имеет первообразную на
имеет первообразную на 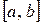 . Тогда ряд
. Тогда ряд  сходится равномерно на
сходится равномерно на 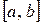 , причем
, причем
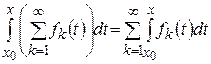 , (9)
, (9)
т.е. ряд можно почленно интегрировать.
‰ Докажем теорему для последовательностей. Положим 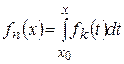 ,
,  . Тогда
. Тогда 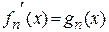 причем
причем
1)  – дифференцируемая функция
– дифференцируемая функция 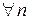 ;
;
2) последовательность 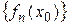 – сходится;
– сходится;
3) последовательность 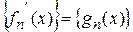 сходится равномерно на
сходится равномерно на 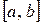 .
.
Следовательно, последовательность 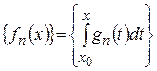 по предыдущей теореме сходится равномерно на
по предыдущей теореме сходится равномерно на 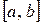 к некоторой функции
к некоторой функции 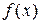 причем
причем
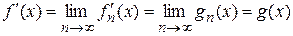 .
.
Отсюда следует, что
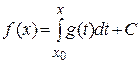 .
.
Таким образом, 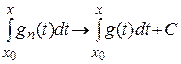 при
при 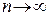 на
на 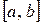 .
.
Подставляя 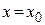 , получаем, что
, получаем, что  . <
. <
Пример 12. Рассмотрим ряд 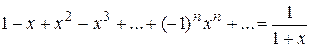 . Он равномерно сходится на
. Он равномерно сходится на 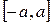 ,
, 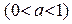 по признаку Вейерштрасса. Тогда его можно почленно интегрировать. Получим:
по признаку Вейерштрасса. Тогда его можно почленно интегрировать. Получим:
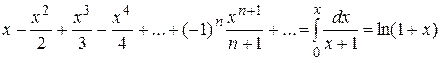 .
.
Так как  любое число из (0, 1), то представление справедливо
любое число из (0, 1), то представление справедливо  . Таким образом, можно приближенно вычислить логарифмы.
. Таким образом, можно приближенно вычислить логарифмы.

 равномерно сходится к функции
равномерно сходится к функции 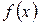 на множестве
на множестве 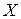 ;
; – предельная точка множества
– предельная точка множества 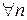 существуют пределы
существуют пределы 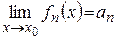 .
.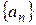 сходится и
сходится и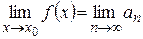 . (4)
. (4)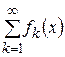 равномерно сходится к
равномерно сходится к 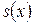 на
на 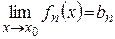 .
.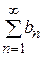 – сходится, причем
– сходится, причем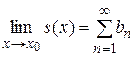 . (5)
. (5)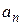 сходится. Т.к.
сходится. Т.к.  сходится равномерно на
сходится равномерно на 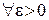
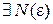 такие, что
такие, что  и
и 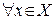 выполняется
выполняется 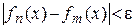 . Переходя к пределу в неравенстве при
. Переходя к пределу в неравенстве при  , так как
, так как 
 , т.е. последовательность фундаментальная, а это означает, что она сходится.
, т.е. последовательность фундаментальная, а это означает, что она сходится.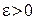 . В силу равномерной сходимости
. В силу равномерной сходимости 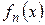 для
для  такое, что
такое, что 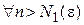 и
и 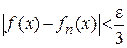 . (6)
. (6)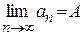 , то для
, то для 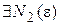 выполняется
выполняется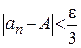 . (7)
. (7) . Для этого N справедливы неравенства (6) и (7). Так как
. Для этого N справедливы неравенства (6) и (7). Так как  , что выполнится
, что выполнится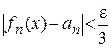 при
при 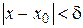 . (8)
. (8) будем иметь из (6) – (8):
будем иметь из (6) – (8): ,
,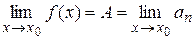 <
<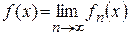 ,
, 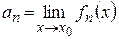 , то (4) можно записать
, то (4) можно записать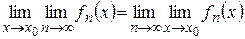 .
. , порядок взятия предела можно изменять.
, порядок взятия предела можно изменять. .
.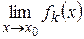 , то операции предельного перехода и суммирования перестановочны.
, то операции предельного перехода и суммирования перестановочны. функций равномерно сходится к
функций равномерно сходится к  на
на 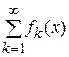 непрерывные на
непрерывные на 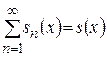 . Надо доказать, что
. Надо доказать, что 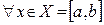 . Возьмем
. Возьмем 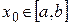 и найдем предел
и найдем предел 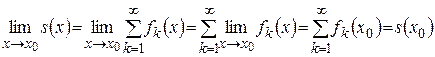 .
.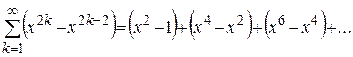 на отрезке
на отрезке 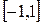 .
.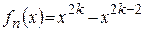 непрерывны на
непрерывны на 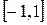 и
и 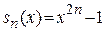 .
.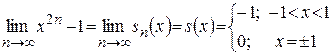 ,
, .
. сходится при некотором
сходится при некотором 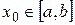 ;
;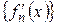 равномерно сходится на
равномерно сходится на  ), причем
), причем ,
,  . (9)
. (9)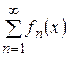 удовлетворяет следующим условиям:
удовлетворяет следующим условиям: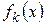 для
для 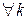 дифференцируема на
дифференцируема на 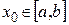 ;
;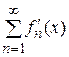 сходится равномерно на
сходится равномерно на 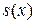 , т.е.
, т.е. 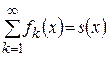 , и причем
, и причем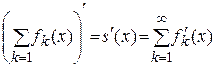 .
.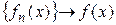 и сходится равномерно на
и сходится равномерно на 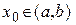 и
и 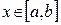 . Из очевидного тождества
. Из очевидного тождества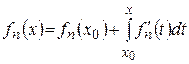 для
для 
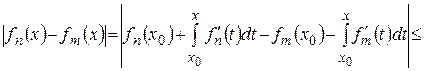
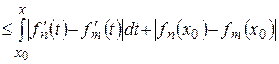 ,
, 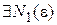 , что при всех
, что при всех 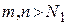 и для
и для 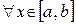 выполнится
выполнится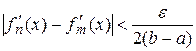 .
.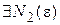 , что для
, что для  выполняется
выполняется .
.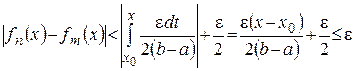
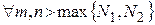 и
и  , следовательно, в силу критерия Коши, последовательность
, следовательно, в силу критерия Коши, последовательность 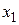 – произвольная точка
– произвольная точка  определенную на множестве
определенную на множестве  и докажем, что она сходится равномерно. Рассмотрим
и докажем, что она сходится равномерно. Рассмотрим  . Применим к
. Применим к 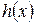 формулу Лагранжа
формулу Лагранжа 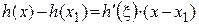
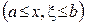 или
или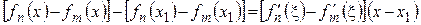 .
.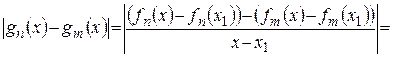
 ,
, , что выполняется
, что выполняется  для
для  в силу равномерной сходимости
в силу равномерной сходимости  . Откуда следует, что последовательность
. Откуда следует, что последовательность 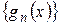 сходится равномерно на
сходится равномерно на  .
.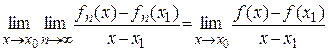 .
.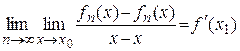 .
.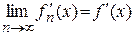 , и по определению производной выполняется
, и по определению производной выполняется 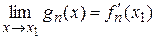 .
.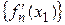 сходится, причем
сходится, причем 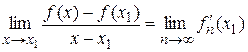 . Так как
. Так как  на отрезке
на отрезке 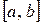 , причем каждая
, причем каждая 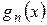 имеет первообразную на
имеет первообразную на 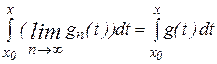 .
. сходится равномерно на
сходится равномерно на 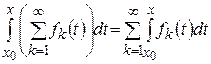 , (9)
, (9)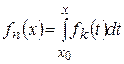 ,
,  . Тогда
. Тогда 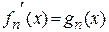 причем
причем – дифференцируемая функция
– дифференцируемая функция 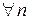 ;
;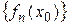 – сходится;
– сходится;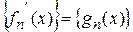 сходится равномерно на
сходится равномерно на 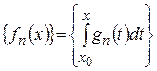 по предыдущей теореме сходится равномерно на
по предыдущей теореме сходится равномерно на 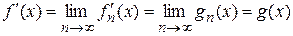 .
.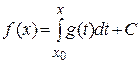 .
.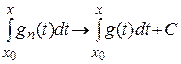 при
при  на
на  , получаем, что
, получаем, что  . <
. <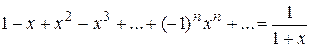 . Он равномерно сходится на
. Он равномерно сходится на 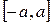 ,
, 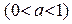 по признаку Вейерштрасса. Тогда его можно почленно интегрировать. Получим:
по признаку Вейерштрасса. Тогда его можно почленно интегрировать. Получим: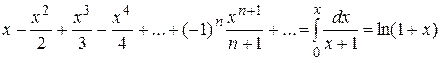 .
. любое число из (0, 1), то представление справедливо
любое число из (0, 1), то представление справедливо  . Таким образом, можно приближенно вычислить логарифмы.
. Таким образом, можно приближенно вычислить логарифмы.