Рассмотрим вопрос о сходимости ряда Фурье. Вначале заметим, что если ряд Фурье 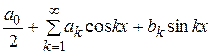 сходится на отрезке
сходится на отрезке  к функции
к функции  , то в силу периодичности его членов он сходится на всей числовой прямой к периодической функции. Эта функция является периодическим продолжением с периодом
, то в силу периодичности его членов он сходится на всей числовой прямой к периодической функции. Эта функция является периодическим продолжением с периодом  функции
функции  . Поэтому будем считать, что на числовой прямой задана периодическая с периодом
. Поэтому будем считать, что на числовой прямой задана периодическая с периодом  функция
функция  , интегрируемая на
, интегрируемая на  и для нее написан ряд Фурье с коэффициентами, определенными по формулам (23).
и для нее написан ряд Фурье с коэффициентами, определенными по формулам (23).
Теорема 15. (Дирихле) Пусть выполняются условия:
1)  периодическая с периодом
периодическая с периодом  функция;
функция;
2)  кусочно-непрерывная на
кусочно-непрерывная на  ;
;
3)  имеет в каждой точке
имеет в каждой точке  правую и левую производные.
правую и левую производные.
Тогда ряд Фурье функции  сходится всюду, причем его сумма в точках непрерывности функции равна
сходится всюду, причем его сумма в точках непрерывности функции равна  , а в точках разрыва равна
, а в точках разрыва равна  .
.
ƒ Вначале получим интегральное представление для частичной суммы  .
.

 .
.
Воспользуемся формулой
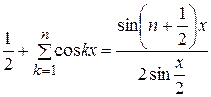 (26)
(26)
и получим
 .
.
Производя замену  , получаем
, получаем
 .
.
Так как под интегралом стоит периодическая с периодом  функция, то интеграл по любому отрезку
функция, то интеграл по любому отрезку  имеет одно и тоже значение
имеет одно и тоже значение

 .
.
Заменяя в первом интеграле  , получаем
, получаем

 . (27)
. (27)
Из (26) следует, что
 .
.
Тогда в силу (27) имеем




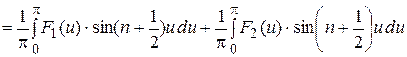 . (27)
. (27)
Функции  и
и  кусочно-непрерывны на
кусочно-непрерывны на  , так как имеют разрывы первого ряда в тех же точках, что и функции
, так как имеют разрывы первого ряда в тех же точках, что и функции  и
и  соответственно. При
соответственно. При 
 и
и  можно считать непрерывными, так как в силу условий теоремы существуют пределы
можно считать непрерывными, так как в силу условий теоремы существуют пределы
 – правая производная.
– правая производная.
 – левая производная.
– левая производная.
Перейдем в (27) к пределу при  . В силу Леммы Римана при
. В силу Леммы Римана при  оба интеграла равны 0. Следовательно, для
оба интеграла равны 0. Следовательно, для  выполняется
выполняется
 .
.
В частности, если  – точка непрерывности функции
– точка непрерывности функции  , то
, то  и
и  . <
. <
Теперь рассмотрим достаточные условия равномерной сходимости тригонометрического ряда Фурье.
Определение 7. Говорят, что функция  имеет на отрезке
имеет на отрезке  кусочно-непрерывную производную, если
кусочно-непрерывную производную, если 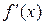 существует и непрерывна на отрезке
существует и непрерывна на отрезке  , за исключением может быть конечного числа точек, в каждой из которых функция
, за исключением может быть конечного числа точек, в каждой из которых функция 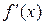 имеет пределы слева и справа.
имеет пределы слева и справа.
Теорема 16. Пусть  непрерывная периодическая (с периодом
непрерывная периодическая (с периодом  ) функция, имеющая на отрезке
) функция, имеющая на отрезке  кусочно-непрерывную производную. Тогда ряд Фурье функции
кусочно-непрерывную производную. Тогда ряд Фурье функции  сходится абсолютно и равномерно на всей числовой прямой.
сходится абсолютно и равномерно на всей числовой прямой.
ƒ По условиям теоремы  имеет кусочно-непрерывную производную, тогда она в каждой точке имеет левую и правую производные, и, таким образом,
имеет кусочно-непрерывную производную, тогда она в каждой точке имеет левую и правую производные, и, таким образом,  удовлетворяет всем условиям теоремы 1 и поэтому ряд Фурье сходится всюду к
удовлетворяет всем условиям теоремы 1 и поэтому ряд Фурье сходится всюду к  . Докажем, что ряд сходится абсолютно и равномерно.
. Докажем, что ряд сходится абсолютно и равномерно.
Пусть  и
и  коэффициенты Фурье функции
коэффициенты Фурье функции 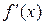 . Тогда
. Тогда

 .
.
Аналогично получаем, что  .
.
Рассмотрим числовой ряд
 .
.
Этот ряд сходится, так как  ,
,  , а ряды
, а ряды 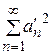 ;
; 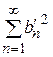 ,
,  – сходятся. Сходимость первых двух рядов следует из неравенства Бесселя
– сходятся. Сходимость первых двух рядов следует из неравенства Бесселя
 .
.
Из сходимости ряда  в силу признака Вейерштрасса следует абсолютная и равномерная сходимость ряда Фурье на всей числовой прямой. <
в силу признака Вейерштрасса следует абсолютная и равномерная сходимость ряда Фурье на всей числовой прямой. <
Замечание. Доказанная теорема естественно переносится на тригонометрические ряды Фурье периодических функций с произвольным периодом.

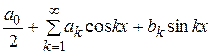 сходится на отрезке
сходится на отрезке  к функции
к функции  , то в силу периодичности его членов он сходится на всей числовой прямой к периодической функции. Эта функция является периодическим продолжением с периодом
, то в силу периодичности его членов он сходится на всей числовой прямой к периодической функции. Эта функция является периодическим продолжением с периодом  функции
функции  .
. .
.
 .
.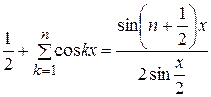 (26)
(26) .
. , получаем
, получаем .
.
 .
. , получаем
, получаем
 . (27)
. (27) .
.



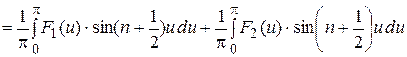 . (27)
. (27) и
и  кусочно-непрерывны на
кусочно-непрерывны на  , так как имеют разрывы первого ряда в тех же точках, что и функции
, так как имеют разрывы первого ряда в тех же точках, что и функции  и
и  соответственно. При
соответственно. При 
 и
и  можно считать непрерывными, так как в силу условий теоремы существуют пределы
можно считать непрерывными, так как в силу условий теоремы существуют пределы – правая производная.
– правая производная. – левая производная.
– левая производная. . В силу Леммы Римана при
. В силу Леммы Римана при  выполняется
выполняется .
. – точка непрерывности функции
– точка непрерывности функции  , то
, то  и
и  . <
. < кусочно-непрерывную производную, если
кусочно-непрерывную производную, если 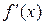 существует и непрерывна на отрезке
существует и непрерывна на отрезке  кусочно-непрерывную производную. Тогда ряд Фурье функции
кусочно-непрерывную производную. Тогда ряд Фурье функции  и
и  коэффициенты Фурье функции
коэффициенты Фурье функции 
 .
. .
. .
. ,
,  , а ряды
, а ряды 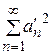 ;
; 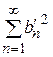 ,
,  – сходятся. Сходимость первых двух рядов следует из неравенства Бесселя
– сходятся. Сходимость первых двух рядов следует из неравенства Бесселя .
.