Свойства коэффициентов Фурье
Коэффициенты ряда Фурье обладают рядом важных свойств. 1. Если
ƒ Известны свойства периодических функций а) б) в) Тогда доказываемые формулы получаются, если в них положить 2. Если Если ƒ По определению: четная функция удовлетворяет условию а) если б) если в) если Тогда, если
Таким образом, Из этого свойства следует, что тригонометрический ряд Фурье для четных функций
где Для нечетных функций тригонометрический ряд Фурье соответственно имеет вид
где Сделанные выводы сохраняются для тригонометрических рядов по системе общего вида. Для четной функции:
где Для нечетной функции:
где 3. Лемма Римана. Если ƒ Пусть Функция
и по теореме Кантора равномерно непрерывна. Следовательно, для
Зададим Произведем оценку интеграла:
Так как
при Откуда следует, что при
Тогда, очевидно, что для кусочно-непрерывной на
Последнее следует из формул (23).
Пример 25. Разложить в ряд Фурье двумя способами функцию, представленную на рис. 11.2 по косинусам и по синусам. Решение. а) Разложение Вычислим коэффициенты ряда Фурье, учитывая, что
Разложение будет иметь вид
б) Разложение
Вычислим коэффициенты ряда Фурье. Так как получившаяся функция
Получаем выражение для ряда Фурье заданной функции
|

 имеет период
имеет период  (например, рис. 11.1), то коэффициенты ряда Фурье для нее вычисляются по следующим формулам
(например, рис. 11.1), то коэффициенты ряда Фурье для нее вычисляются по следующим формулам
 ,
,  ,
,  .
. ;
; ;
; .
. ,
,  . <
. < для
для  .
. нечетная функция, то
нечетная функция, то  ,
,  для
для  , а нечетная
, а нечетная 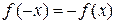 . Известно, что:
. Известно, что: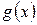 четные функции, то
четные функции, то  – четная;
– четная; – нечетная, т.к.
– нечетная, т.к.  нечетная.
нечетная.

 .
. ,
, ,
,  ,
, 
 ,
, ,
,  ,
,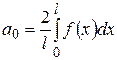 ,
,  .
. ,
, .
. , то
, то  ,
,  .
. ,
,  , …,
, …,  точки разрыва функции
точки разрыва функции  и
и  по каждому из отрезков
по каждому из отрезков  ,
,  , …,
, …,  стремятся к нулю при
стремятся к нулю при  . Пусть
. Пусть  один из таких отрезков,
один из таких отрезков,  .
. для
для  (24)
(24)
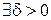 такое, что для
такое, что для  выполняется
выполняется  , тогда
, тогда для
для  и выберем на
и выберем на  с шагом
с шагом  разбиение
разбиение  так, чтобы
так, чтобы  ,
,  и
и  .
.
 .
. , то из (24) и (25) имеем
, то из (24) и (25) имеем ,
, .
. имеем
имеем , т.е.
, т.е.  функции
функции  .
.
 , определенную на
, определенную на  и совпадающую с
и совпадающую с  .
.
 .
.

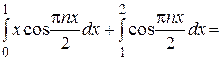
 .
.
 .
.

 .
. .
.


