Интеграл Фурье
Пусть функция
где Интеграл (31) аналогичен ряду Фурье периодической функции, только суммирование заменено интегрированием. Подставим (32) в (31), получим
Определение 8. Интеграл
называется интегралом Фурье функции Подобно тому, как при некоторых условиях периодическая функция раскладывается в ряд Фурье, так и при некоторых условиях Теорема 17. Пусть: 1) 2) 3) интеграл Тогда при любом
(Без доказательства.) Вспомним понятие главного значения несобственного интеграла на действительной оси. Если v.p. где v.p. сокращение от value principle. Отличие интеграла, стоящего справа, от интеграла слева в равенстве (35), состоит в том, что Например, Пусть функция
Отсюда, в силу четности косинуса, следует, что
Рассмотрим функцию
Она непрерывна и абсолютно интегрируема по признаку Вейерштрасса, так как v.p. Тогда
Перепишем полученное равенство
Определение 9. Отображение F, ставящее в соответствие функции
называется преобразованием Фурье. Отображение Контрольные вопросы 1. Что называется функциональным рядом? Дайте определения сходящегося и равномерно сходящегося функциональных рядов. В чем состоит отличие? 2. Сформулируйте критерий Коши и признак Вейерштрасса для функциональных рядов. Приведите примеры применения. 3. Сформулируйте теорему о пределе суммы функционального ряда и теорему об её непрерывности. Приведите пример ряда с непрерывными функциями, у которого сумма является разрывной функцией. 4. Сформулируйте теоремы о дифференцировании и интегрировании функционального ряда. Приведите примеры применения. 5. Какой функциональный ряд называется степенным? Сформулируйте теорему Коши-Адамара. Какое множество является областью сходимости степенного ряда? Как его находят? 6. Сформулируйте теорему Абеля и теорему о почленном дифференцировании и интегрировании степенного ряда. Приведите пример применения последней теоремы. 7. Какой степенной ряд называется рядом Тейлора? Как определяются коэффициенты этого ряда? 8. В чем состоит необходимое и достаточное условие сходимости 9. Запишите разложения следующих функций в ряд Маклорена: 10. Что называется основной тригонометрической системой и тригонометрической системой общего вида? Что означает ортогональность этих систем? 11. Запишите тригонометрический ряд Фурье и коэффициенты Фурье по основной тригонометрической системе и по тригонометрической системе общего вида. 12. Сформулируйте свойства коэффициентов Фурье, а также лемму Римана. 13. Запишите тригонометрический ряд Фурье и коэффициенты Фурье: а) для четных функций; б) для нечетных функций 14. Сформулируйте теорему Вейерштрасса. Какими свойствами должна обладать функция, чтобы абсолютно и равномерно сходился ее ряд Фурье? 15. Запишите тригонометрический ряд Фурье в комплексной форме и коэффициенты Фурье. Приведите пример. 16. Какой вид имеет интеграл Фурье? При каких условиях интеграл Фурье сходится? Запишите интегральное преобразование Фурье.
|

 задана на всей числовой прямой
задана на всей числовой прямой  и абсолютна интегрируема на ней. Составим для
и абсолютна интегрируема на ней. Составим для  заменено интегрированием по параметру
заменено интегрированием по параметру  :
: , (31)
, (31) ,
,  . (32)
. (32)
 .
. (33)
(33) кусочно-непрерывная на любом
кусочно-непрерывная на любом  числовой прямой;
числовой прямой; и
и  для
для  ;
; сходится.
сходится. имеет место равенство
имеет место равенство . (34)
. (34) числовой прямой
числовой прямой  (т.е. локально интегрируема), тогда
(т.е. локально интегрируема), тогда , (35)
, (35) является пределом интегралов
является пределом интегралов  при произвольном стремлении
при произвольном стремлении  ,
,  , а интеграл (35) предел тех же интегралов, но при
, а интеграл (35) предел тех же интегралов, но при  и
и 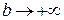 . Если существует несобственный интеграл, то существует и интеграл в смысле v.p., но не наоборот.
. Если существует несобственный интеграл, то существует и интеграл в смысле v.p., но не наоборот. не существует, а v.p.
не существует, а v.p.  .
. односторонние производные, тогда по теореме 15
односторонние производные, тогда по теореме 15 .
. .
.
 , а
, а  – абсолютно интегрируема. В силу нечетности синуса
– абсолютно интегрируема. В силу нечетности синуса  также нечетная, поэтому
также нечетная, поэтому .
.

 .
. .
. (или
(или  ), определяемое формулой
), определяемое формулой
 , ставящее в соответствие функции
, ставящее в соответствие функции  , функцию
, функцию  , определяемую формулой
, определяемую формулой  называется обратным преобразованием Фурье. Из формулы ясно, что
называется обратным преобразованием Фурье. Из формулы ясно, что  .
. к своему ряду Тейлора? Только достаточное? Приведите пример функции, к которой не сходится её ряд Тейлора.
к своему ряду Тейлора? Только достаточное? Приведите пример функции, к которой не сходится её ряд Тейлора. .
.


