Ряд Тейлора
Пусть функция
интервал сходимости которого есть Найдем коэффициенты
......................
Положим
Откуда коэффициенты ряда
Подставляя в (15) получим ряд
Полученный ряд (16) называется рядом Тейлора для функции В частности, если
Таким образом, если степенной ряд
В этом случае говорят, что функция Ясно, что если Поставим обратную задачу. Пусть Теорема 12. Для того чтобы бесконечно дифференцируемая функция в окрестности точки
‰ Запишем формулу Тейлора в окрестности точки где Ясно, что ряд Тейлора представляет собой бесконечное удлинение функции Тейлора. Необходимость. Обозначим частичную сумму ряда
Тогда из формулы Тейлора получаем Пусть Достаточность. Пусть, Непосредственная проверка выполнения условия (18) обычно бывает довольно сложной. Сформулируем достаточное условие сходимости ряда (16) к Теорема 13. Пусть функция
тогда ряд (16) сходится к ‰ Надо показать, что при сделанных предположениях в теореме выполняется условие (18). Из формулы
следует, что Следствие. Пусть все производные Заметим, что ряд Тейлора не всегда сходится к той функции, для которой он написан. Пример 16. (Адамар) Функция Получим разложение некоторых элементарных функций в степенные ряды. Показательная функция
При
На произвольном интервале Функция
Получаем Все ее производные ограничены в совокупности на всей числовой прямой
Следовательно, формула
справедлива при всех Функция
вывод аналогичный. Областью сходимости являетсяснова вся числовая прямая. Степенная функция
…
Вычисляя
По признаку Даламбера легко показать, что областью сходимости биномиального ряда является интервал Если
Стандартным путем разложения известной функции в степенной ряд является следующий: вычисляют производные, формально составляют ряд Тейлора и смотрят, сходится или не сходится ряд к Логарифмическая функция
Интервал сходимости Функция
Интервал сходимости Для разложений функций в степенные ряды обычно используют эти разложения, а также разложения
Пример 17. Разложить в ряд Решение. Так как
Пример 18. Разложить в ряд Решение. Так как
Пример 19. Разложить в ряд Решение. Воспользуемся формулой понижения степени и представим исходную функцию следующим образом
Воспользуемся известным разложением в ряд функции
Пример 20. Разложить в ряд Решение. Преобразуем выражение для функции и воспользуемся известным разложением для
Пример 21. Разложить в ряд Решение. Представим исходную функцию следующим образом
Вычислим коэффициенты ряда:
Получаем ряд
Пример 22. Разложить в ряд функцию Решение. Воспользуемся формулой (9). Учитывая, что
Замечание. Разложение функции в степенные ряды используют для решения многих задач: вычисления пределов; нахождения интегралов; приближенное вычисление значений функции; приближенного вычисления определенных интегралов; приближенного решения дифференциальных уравнений и т.д. Пример 23. Вчислить интеграл с точностью δ=0,001:
|

 является суммой степенного ряда
является суммой степенного ряда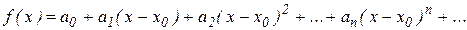 , (15)
, (15) .
. . В интервале сходимости ряд можно почленно дифференцировать, причем получится ряд, сходящийся в этом интервале. Продифференцируем последовательно ряд
. В интервале сходимости ряд можно почленно дифференцировать, причем получится ряд, сходящийся в этом интервале. Продифференцируем последовательно ряд  раз
раз ,
, ,
, ,
,

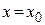 в этих тождествах.
в этих тождествах. ;
;  ;
;  ;
;  ;
;  .
.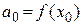 ,
,  ,
,  ,…,
,…,  .
.
 (16)
(16) , то этот ряд называется рядом Маклорена.
, то этот ряд называется рядом Маклорена.
 имеет сумму
имеет сумму  ,
,  (17)
(17) или по степеням
или по степеням  . Очевидно, что ряд Тейлора является бесконечным продолжением формулы Тейлора.
. Очевидно, что ряд Тейлора является бесконечным продолжением формулы Тейлора. число раз дифференцируема.
число раз дифференцируема.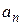 по формулам (17). Возникает вопрос: будет ли сумма данного ряда Тейлора совпадать с функцией
по формулам (17). Возникает вопрос: будет ли сумма данного ряда Тейлора совпадать с функцией 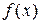 , для которой он составлен?
, для которой он составлен? в формуле Тейлора для функции
в формуле Тейлора для функции 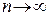 , т.е.
, т.е.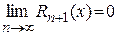 (18)
(18)
 ,
, ,
,  остаточный член в формуле Лагранжа.
остаточный член в формуле Лагранжа. .
. ,
,  .
. . Тогда из
. Тогда из  ,
,  .
. . Из
. Из  следует, что
следует, что  , т.е.
, т.е.  .
. и
и  , что выполняется
, что выполняется ,
,  и
и  , (19)
, (19)
 . Но
. Но  (известно из теоремы пределов). Тогда условие (18) выполняется и из теоремы 12 следует, что теорема доказана. <
(известно из теоремы пределов). Тогда условие (18) выполняется и из теоремы 12 следует, что теорема доказана. < ограничены в совокупности в интервале
ограничены в совокупности в интервале  и
и  , т.е.
, т.е.  для
для  и
и  . Тогда ряд Тейлора сходится к
. Тогда ряд Тейлора сходится к  бесконечное число раз дифференцируема. Если
бесконечное число раз дифференцируема. Если  , то
, то  и функция, очевидно, дифференцируемая. При
и функция, очевидно, дифференцируемая. При  производные вычисляются по определению, причем
производные вычисляются по определению, причем 
 . Отсюда
. Отсюда  и ясно, что полученный ряд тождественно равен нулю и не сходится к функции
и ясно, что полученный ряд тождественно равен нулю и не сходится к функции  .
. ,
,  .
. ,
,  .
. .
. ряд Тейлора имеет вид:
ряд Тейлора имеет вид:

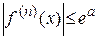 для
для  и
и  . Тогда по следствию ряд сходится к
. Тогда по следствию ряд сходится к  . Так как число
. Так как число  произвольное, то ряд сходится на всей числовой прямой.
произвольное, то ряд сходится на всей числовой прямой. ,
,  – бесконечно число раздифференцируемая.
– бесконечно число раздифференцируемая. ,
,  ,
,  ,
,  , …
, … ,
,  ,
,  ,
,  ,
, 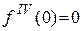 , …
, … так как
так как .
.
 , т.е. степенной ряд сходится для
, т.е. степенной ряд сходится для  .
. ,
, 
 ,
, 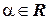 ,
,  ,
, 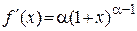 ,
, ,
, .
. .
. , получим степенной ряд Маклорена, который называется биномиальным рядом:
, получим степенной ряд Маклорена, который называется биномиальным рядом:
 . Поведение при
. Поведение при  зависит от
зависит от  . Показано, что
. Показано, что  при
при  .
. – натуральное число, то все коэффициенты при степенях
– натуральное число, то все коэффициенты при степенях  при
при  равны нулю и разложение превращается в формулу бинома Ньютона, верную при всех
равны нулю и разложение превращается в формулу бинома Ньютона, верную при всех 
 .
. и
и  с помощью дифференцирования и интегрирования известного степенного ряда.
с помощью дифференцирования и интегрирования известного степенного ряда.
 .
. . Это легко показать по признаку Даламбера.
. Это легко показать по признаку Даламбера. .
.
 ,
,  , справедливые при
, справедливые при 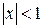 .
. по степеням х.
по степеням х. , то можно воспользоваться разложением в ряд для функции
, то можно воспользоваться разложением в ряд для функции  .
.

 по степеням х.
по степеням х. , то можно воспользоваться разложением в ряд для функции
, то можно воспользоваться разложением в ряд для функции 

 по степеням х.
по степеням х.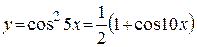 .
. , получим
, получим

 .
. по степеням
по степеням  .
.


 по степеням
по степеням  .
. ,
, ,
, ,
, ,
, , …
, …
 .
.

 по степеням
по степеням  . Указание
. Указание  .
. , получаем
, получаем

 .
.



