Краткая теория. Конвективным теплообменом или теплоотдачей называется процесс переноса теплоты между поверхностью твердого тела и жидкой средой

Конвективным теплообменом или теплоотдачей называется процесс переноса теплоты между поверхностью твердого тела и жидкой средой. При этом перенос теплоты осуществляется одновременным действием теплопроводности и конвекции.

Здесь процесс переноса теплоты неразрывно связан с переносом самой среды. По природе возникновения различают два вида движения — свободное и вынужденное.

Свободным называется движение, происходящее вследствие разности плотностей нагретых и холодных частиц жидкости в гравитационном поле. Интенсивность свободного движения определяется тепловыми условиями процесса и зависит от рода жидкости, разности температур, напряженности гравитационного поля и объема пространства, в котором протекает процесс. Свободное движение называется также естественной конвекцией.

Вынужденным называется движение, возникающее под действием посторонних возбудителей, например насоса, вентилятора и пр.

Интенсивность конвективного теплообмена характеризуется коэффициентом теплоотдачи α;, который определяется по формуле Ньютона—Рихмана:

Q = α (tc – tж)F.

(1)

Согласно этому закону, тепловой поток Q пропорционален по­верхности теплообмена F и разности температур стенки и жидкости (t_c – t_ж).

Коэффициент теплоотдачи можно определить как количество теплоты, отдаваемое в единицу времени единицей поверхности при разности температур между поверхностью и жидкостью, равной одному градусу:

α = .

(2)

Процессы теплоотдачи во многом определяются условиями движения жидкости. Как известно, имеются два основных режима течения: ламинарный и турбулентный.

Режим движения рабочей жидкости определяет механизм переноса теплоты. При ламинарном режиме перенос теплоты в направлении нормали к стенке в основном осуществляется путем теплопроводности. При турбулентном режиме такой способ переноса теплоты сохраняется лишь в вязком подслое, а внутри турбулентного ядра перенос осуществляется путем интенсивного перемешивания частиц жидкости. В этих условиях для газов и обычных жидкостей интенсивность теплоотдачи в основном определяется термическим сопротивлением пристенного подслоя, которое по сравнению с термическим сопротивлением ядра оказывается определяющим. В этом легко убедиться, если проследить за изменением температуры жидкости в направлении нормали к стенке (рисунок на титульном листе).

Как видно, наибольшее изменение температуры происходит в пределах тонкого слоя у поверхности, через который теплота передается путем теплопроводности.

Процесс теплоотдачи является сложным процессом, а коэффициент теплоотдачи является сложной функцией различных величин, характеризующих этот процесс. В общем случае коэффициент теплоотдачи является функцией формы Ф, размеров l₁, l₂..., температуры поверхности нагрева t_c, скорости жидкости ω;, ее температуры t_ж, физических свойств жидкости – коэффициента теплопроводности λ;, удельной теплоемкости с_р, плотности ρ;, ко­эффициента вязкости μ; и других факторов:

α = f(ω, tc, tж, λ, cp, ρ, μ, а, Φ, lt,l2...).

(3)

В качестве теплоносителей в настоящее время применяются самые разнообразные вещества – воздух, газы, вода, масла, бензол, нефть, бензин, спирты, расплавленные металлы и различные специальные смеси. Для каждого теплоносителя физические свойства имеют определенные значения и, как правило, являются функцией температуры, а некоторые – и давления.

Наиболее точно α; можно определить, используя математическое описание процесса теплоотдачи, состоящего: 1) из уравнения теплопроводности; 2) уравнения движения; 3) уравнения сплошности; 4) уравнения теплоотдачи; 5) условий однозначности (геометрические, физические, граничные, временные).

К настоящему времени аналитические решения системы дифференциальных уравнений конвективного теплообмена получены лишь для ограниченного числа простейших задач и то при целом ряде допущений. Такое положение объясняется большой сложностью этих уравнений.

С достаточной для инженерных расчетов точностью α; можно определять опытным путем. Но и этот способ представляет собой нелегкую задачу, особенно для сложных и громоздких тепловых устройств. Кроме того, полученные опытным путем значения α;, строго говоря, нельзя применять при расчете других аппаратов.

Задача значительно упрощается, если опытное определение α производится на моделях, более удобных для экспериментирования. Результаты, полученные на моделях, обобщают, используя тепловую теорию подобия.

Числа подобия можно получить для любого физического явления исходя из математического описания подобных процессов.

1. Числа подобия. Числам подобия присвоены имена ученых, сделавших большие открытия в области теплообмена и гидродинамики. Такие числа обозначаются одной или двумя начальными буквами фамилий этих ученых.

Число Нуссельта (Nu). Это число подобия определяет интенсивность конвективного теплообмена на границе «стенка—жидкость». Чем интенсивнее происходит конвективный теплообмен, тем больше число Nu и тем больше коэффициент теплоотдачи α, что видно из следующей формулы:

Nu = αl0/λ,

(4)

где α — коэффициент теплоотдачи, Вт/ (м² · К); λ — теплопроводность жидкости, Вт/ (м · К); l₀ — определяю­щий линейный размер, м.

Определяющим называется размер, которым определя­ется развитие процесса теплообмена. Если жидкость, уча­ствующая в теплообмене, протекает в круглой трубе, то оп­ределяющим размером является d — внутренний диаметр трубы. При поперечном обтекании трубы или пучка труб в уравнение (4)

Рис.1. К определению dэкв

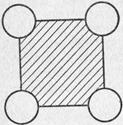
подставляется вместо l₀ значение наруж­ного диаметра трубы или труб. Если сечение канала, по которому течет жидкость, сложной формы, то опреде­ляющим размером является так на­зываемый эквивалентный диаметр l₀ = d_экв = 4F/П, где F — площадь поперечного сечения канала; П — смоченный периметр канала. Напри­мер, если жидкость протекает вдоль труб, расположенных рядами, то F равна заштрихованной площади, как показано на рис. 1.

При продольном обтекании пли­ты определяющим размером являет­ся ее длина l, т. е. l₀ = l.

Число Рейнольдса (Re). Число подобия Рейнольдса определяет характер движения жидкости:

Re = ω0l0/ν,

(5)

где ω₀ — средняя (линейная) скорость жидкости, м/с;

ν — кинематическая вязкость жидкости, м²/с.

Движение жидкости остается ламинарным, пока безраз­мерное число Рейнольдса меньше 2320 (Re < 2320). При Re > 10 000 режим движения жидкости считается турбу­лентным. При числах Рейнольдса больше 2320 и меньше 10 000 — режим переходный от ламинарного к турбулент­ному, т. е. по своему характеру неустойчивый.

Число Прандтля (Рг). Это число подобия оп­ределяет физические свойства жидкости:

Pr = ν/ а,

(6)

где а — температуропроводность жидкости, м²/с.

Значение числа Рг идеальных газов зависит только от их атомности. Число Рг для идеальных газов: одноатомных.... 0,67 двухатомных.... 0,72 трехатомных.... 0,80

Зависимость числа Рг реальных газов от температуры очень незначительна.

Число Рг капельных жидкостей заметно изменяется толь­ко в пределах температур от 0 и примерно до 130°С (с рос­том температуры число Рг увеличивается). При температурах выше 130°С число Рг изменяется незначительно и его мож­но принять равным 1. Зависимость Рг от давления стано­вится заметной только при состояниях жидкости, близких к критическому.

Число Пекле (Ре). Число Пекле является произ­ведением чисел подобия Re и Рг:

Ρ e = Re·Pr = ωl0/ а.

(7)

Число Грасгофа (Gr). Число подобия Грасгофа определяет соотношение подъемной силы, вызываемой разностью плотностей холодных и нагретых частиц жидко­сти, и сил молекулярного трения. Другими словами, чис­ло Gr характеризует интенсивность свободного движения жидкости:

Gr = βgl30 Δt/ν2,

(8)

где β — температурный коэффициент объемного расшире­ния, К^-1 (для идеальных газов β = 1/273,15 К^-1);

g — ус­корение свободного падения, м/с²;

Δt — разность между определяющими температурами жидкости и стенки, °С.

Число Фурье характеризует временное подобие в нестационарных процессах конвективного теплообмена:

Fо = ,

(9)

где t - время, с.

Большинство величин, входящих в числа подобия конвективного теплообмена, зависят от температуры. Поэтому необходимо, чтобы значения всех этих величин были отнесены к какой-то одной опреде­ляющей температуре. Такой температурой мо­жет быть температура стенки, обозначаемая t_cт, или сред­няя температура потока жидкости, обозначаемая t_ж.

Если отношение температур жидкости при входе в ка­нал t_ж,1 и при выходе из него t_ж,2меньше 2, то средняя тем­пература жидкости по длине канала t_ж может определять­ся как средняя арифметическая температура:

tж = 0,5(tж,1+tж,2).

(10)

При значительной разности температур t_ж,1 и t_ж,2в ка­честве средней температуры жидкости принимается средняя логарифмическая температура:

tж = .

(11)

Здесь Δt_вх и Δt_вых — разности температур жидкости и стенки соответственно при входе в канал и при выходе из него.

Чтобы указать, какая тем­пература принята в каждом конкретном случае в качестве определяющей, в числа подобия вводится соответст­вующий индекс («ст» или «ж»). Часто в индексе указывается также определяющий размер: l или h— при вертикаль­ной стенке или диаметр d(действительный или эквивалент­ный). Поэтому числа подобия могут быть написаны, например, так: Re_d,ж, Nu_l,ст, Nu_h,_ж и т.п.
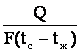
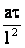