Выполнение работы. Производная . В соответствии с условием достижимости (4.3.12) и функцией делаем вывод
Проиллюстрируем методику синтеза адаптивной системы на основе алгоритма скоростного градиента на простейшем примере, где управляемый объект ― неустойчивое апериодическое звено
Производная 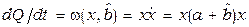 . В соответствии с условием достижимости (4.3.12) и функцией . В соответствии с условием достижимости (4.3.12) и функцией 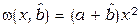 делаем вывод, что при делаем вывод, что при   (выбор числа (выбор числа  зависит от значений коэффициента зависит от значений коэффициента 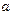 ) существует ) существует 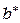 такое, что такое, что 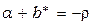 . Следовательно, выполнимо предельное неравенство (4.3.12); в данном случае . Следовательно, выполнимо предельное неравенство (4.3.12); в данном случае 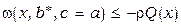 или или 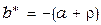 . Алгоритм адаптации на основе алгоритма скоростного градиента принимает вид . Алгоритм адаптации на основе алгоритма скоростного градиента принимает вид 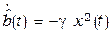 , а система уравнений адаптивной системы включает три уравнения: , а система уравнений адаптивной системы включает три уравнения:
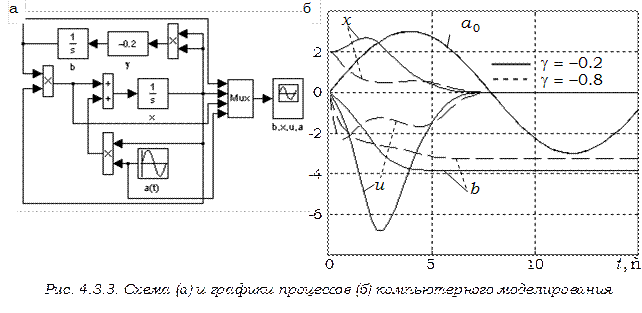
Соответствующая структурная схема системы изображена на рис. 4.3.2.
На рис. 4.3.3, а, б приведены схема и графики переходных процессов в адаптивной системе (рис. 4.3.2). Моделирование выполнено с использованием системы SIMULINK пакета программ MATLAB® . Начальные условия при моделировании приняты следующие: Значение коэффициента изменяется как функция Содержание отчета 1. Структурная схема системы управления. 2) Результаты моделирования
|

 ,
, 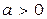 . Ставится задача стабилизации этого неустойчивого звена с целью управления
. Ставится задача стабилизации этого неустойчивого звена с целью управления  при
при  . Для этого примем оценочную функцию
. Для этого примем оценочную функцию  . Целевое условие формально соответствует предельному равенству
. Целевое условие формально соответствует предельному равенству  . Следуя методу скоростного градиента, примем
. Следуя методу скоростного градиента, примем  . Тогда уравнение обобщенного настраиваемого объекта примет вид:
. Тогда уравнение обобщенного настраиваемого объекта примет вид:  .
.
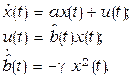
 и
и  для приведенных в примере функций
для приведенных в примере функций  очевидным образом выполняются. Условие выпуклости выполняются в силу линейности
очевидным образом выполняются. Условие выпуклости выполняются в силу линейности  по
по  : из (4.3.11) следует:
: из (4.3.11) следует:  ; в данном случае неравенство (нестрогое) выполняется, так как
; в данном случае неравенство (нестрогое) выполняется, так как  ― тождество. Таким образом, можно сделать вывод, что структура регулятора в обобщенном настраиваемом объекте
― тождество. Таким образом, можно сделать вывод, что структура регулятора в обобщенном настраиваемом объекте  выбрана правильно. Цель управления достигается:
выбрана правильно. Цель управления достигается:  при
при  . Отметим, в алгоритме адаптации используется измеряемая переменная
. Отметим, в алгоритме адаптации используется измеряемая переменная  и отсутствует неизвестный параметр
и отсутствует неизвестный параметр  объекта управления.
объекта управления. .
. , где
, где  . На рис. 4.3.3, б изображены два семейства графиков, полученных при значениях
. На рис. 4.3.3, б изображены два семейства графиков, полученных при значениях  и
и  и иллюстрирующих влияние коэффициента
и иллюстрирующих влияние коэффициента  на сходимость алгоритма скоростного градиента в данном примере.
на сходимость алгоритма скоростного градиента в данном примере.


