В исследуемом типе адаптивных систем прямого действия ставится задача воспроизведения заданной функции  на выходе минимально - фазового объекта управления с уравнением вход-выход вида:
на выходе минимально - фазового объекта управления с уравнением вход-выход вида:
 (3.2.1)
(3.2.1)
Эталонное движение, определяющее требуемую реакцию объекта на задающие воздействия  , определим порождающим уравнением вида:
, определим порождающим уравнением вида:
 (3.2.2)
(3.2.2)
В данном случае эталонная модель движения есть решение уравнения (3.2.2) того же порядка, что и уравнение (3.2.1). Однако это не является обязательным в постановке задачи. В уравнении (3.2.2) сигнал  ― задающее или воспроизводимое воздействие на входе основного контура адаптивной системы. Коэффициенты
― задающее или воспроизводимое воздействие на входе основного контура адаптивной системы. Коэффициенты 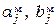 выбираются такими, что полином
выбираются такими, что полином
 (3.2.3)
(3.2.3)
– гурвицев;  для
для  и полином
и полином 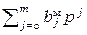 также гурвицев.
также гурвицев.
С введением желаемой и устойчивой эталонной траектории движения  цель управления задается предельным равенством:
цель управления задается предельным равенством:
 . (3.2.4)
. (3.2.4)
Покажем, что такое управление существует и определим закон, которому оно подчиняется. Для этого их (3.2.1) вычтем (3.2.2) и добавим к обеим частям получившейся разности  . Тогда с учетом того, что
. Тогда с учетом того, что  , получим следующее соотношение:
, получим следующее соотношение:
 (3.2.5)
(3.2.5)
Из (3.2.5) следует, что при управлении  , удовлетворяющему дифференциальному уравнению:
, удовлетворяющему дифференциальному уравнению:
 (3.2.6)
(3.2.6)
где  ,
,  ;
;  ,
,  следует
следует  . Так как полином
. Так как полином  – гурвицев, то
– гурвицев, то  и целевое условие выполняется. Таким образом, цель управления, заданная предельным равенством (3.2.4), может быть переформулирована в виде эквивалентного условия на выбор параметров алгоритма управления (2.2.6). Структура адаптивной системы управления в соответствие с уравнением (2.2.6) изображена на рис. 3.2.1.
и целевое условие выполняется. Таким образом, цель управления, заданная предельным равенством (3.2.4), может быть переформулирована в виде эквивалентного условия на выбор параметров алгоритма управления (2.2.6). Структура адаптивной системы управления в соответствие с уравнением (2.2.6) изображена на рис. 3.2.1.
Обозначим вектор параметров идеального регулятора

 , где
, где  . Как видно, настраиваемыми должны быть
. Как видно, настраиваемыми должны быть  параметров согласно условиям:
параметров согласно условиям:
 (3.2.7)
(3.2.7)
и  – “новое” управление:
– “новое” управление:  .
.
Часть параметров регулятора  . При настройке параметров регулятора
. При настройке параметров регулятора 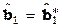 , соответствующих условиям (3.2.7) и называемых далее "идеальными", достигается цель управления (3.2.4). Регулятор с настройками
, соответствующих условиям (3.2.7) и называемых далее "идеальными", достигается цель управления (3.2.4). Регулятор с настройками  также будем называть идеальным регулятором. Его структурная схема изображена на рис. 3.2.1, а. На рис. 3.2.1, б основной контур “свернут” в обобщенный настраиваемый объект, для настройки которого в блоке алгоритмов адаптации используются измеряемые переменные
также будем называть идеальным регулятором. Его структурная схема изображена на рис. 3.2.1, а. На рис. 3.2.1, б основной контур “свернут” в обобщенный настраиваемый объект, для настройки которого в блоке алгоритмов адаптации используются измеряемые переменные  ,
,  и
и  .
.
На рис. 3.2.1 обозначены операторные функции:


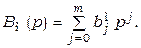
Так как в структуре "идеального" регулятора оператор  является характеристическим полиномом, то становится понятным требование минимально-фазовости полинома
является характеристическим полиномом, то становится понятным требование минимально-фазовости полинома  в уравнении ОУ (3.2.1).
в уравнении ОУ (3.2.1).

 на выходе минимально - фазового объекта управления с уравнением вход-выход вида:
на выходе минимально - фазового объекта управления с уравнением вход-выход вида: (3.2.1)
(3.2.1) (3.2.2)
(3.2.2)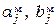 выбираются такими, что полином
выбираются такими, что полином (3.2.3)
(3.2.3) для
для  и полином
и полином 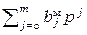 также гурвицев.
также гурвицев. цель управления задается предельным равенством:
цель управления задается предельным равенством: . (3.2.4)
. (3.2.4) . Тогда с учетом того, что
. Тогда с учетом того, что  , получим следующее соотношение:
, получим следующее соотношение: (3.2.5)
(3.2.5) , удовлетворяющему дифференциальному уравнению:
, удовлетворяющему дифференциальному уравнению: (3.2.6)
(3.2.6) ,
,  ;
;  ,
,  следует
следует  . Так как полином
. Так как полином  – гурвицев, то
– гурвицев, то  и целевое условие выполняется. Таким образом, цель управления, заданная предельным равенством (3.2.4), может быть переформулирована в виде эквивалентного условия на выбор параметров алгоритма управления (2.2.6). Структура адаптивной системы управления в соответствие с уравнением (2.2.6) изображена на рис. 3.2.1.
и целевое условие выполняется. Таким образом, цель управления, заданная предельным равенством (3.2.4), может быть переформулирована в виде эквивалентного условия на выбор параметров алгоритма управления (2.2.6). Структура адаптивной системы управления в соответствие с уравнением (2.2.6) изображена на рис. 3.2.1.
 , где
, где  . Как видно, настраиваемыми должны быть
. Как видно, настраиваемыми должны быть  параметров согласно условиям:
параметров согласно условиям: (3.2.7)
(3.2.7) – “новое” управление:
– “новое” управление:  .
. . При настройке параметров регулятора
. При настройке параметров регулятора 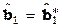 , соответствующих условиям (3.2.7) и называемых далее "идеальными", достигается цель управления (3.2.4). Регулятор с настройками
, соответствующих условиям (3.2.7) и называемых далее "идеальными", достигается цель управления (3.2.4). Регулятор с настройками  также будем называть идеальным регулятором. Его структурная схема изображена на рис. 3.2.1, а. На рис. 3.2.1, б основной контур “свернут” в обобщенный настраиваемый объект, для настройки которого в блоке алгоритмов адаптации используются измеряемые переменные
также будем называть идеальным регулятором. Его структурная схема изображена на рис. 3.2.1, а. На рис. 3.2.1, б основной контур “свернут” в обобщенный настраиваемый объект, для настройки которого в блоке алгоритмов адаптации используются измеряемые переменные  .
.


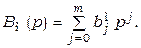
 является характеристическим полиномом, то становится понятным требование минимально-фазовости полинома
является характеристическим полиномом, то становится понятным требование минимально-фазовости полинома  в уравнении ОУ (3.2.1).
в уравнении ОУ (3.2.1).


