Метод скоростного градиента (СГ) применяется для параметрического управления обобщенным настраиваемым объектом, заданным свои уравнением состояния:
 , (4.3.1)
, (4.3.1)
где  ― гладкая функция своих аргументов, линейно зависимая от настраиваемых параметров
― гладкая функция своих аргументов, линейно зависимая от настраиваемых параметров 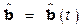 . Локальныйнеотрицательный функционал настройки
. Локальныйнеотрицательный функционал настройки  явно зависит от фазовых координат
явно зависит от фазовых координат  и не зависит явно от настраиваемых параметров
и не зависит явно от настраиваемых параметров  . Полная производная по времени
. Полная производная по времени  вычисляется очевидным образом с учетом уравнения (4.3.1):
вычисляется очевидным образом с учетом уравнения (4.3.1):
 (4.3.2)
(4.3.2)
В данном случае примем, что функционал  явно от времени не зависит. Тогда градиент
явно от времени не зависит. Тогда градиент  по настраиваемым параметрам
по настраиваемым параметрам  принимает вид:
принимает вид:
 (4.3.3)
(4.3.3)
Алгоритм скоростного градиента (СГ) определяет процедуру изменения настраиваемого вектора параметров 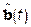 , в соответствии с дифференциальным уравнением первого порядка – алгоритмом градиентного метода:
, в соответствии с дифференциальным уравнением первого порядка – алгоритмом градиентного метода:
 (4.3.4)
(4.3.4)
Интегрируя (2.3.4) на интервале времени  , получаем алгоритм СГ с интегральным оператором
, получаем алгоритм СГ с интегральным оператором 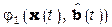 . Структура обобщенного настраиваемого объекта с алгоритмом управления
. Структура обобщенного настраиваемого объекта с алгоритмом управления  (4.3.4) изображена на рис. 4.3.1.
(4.3.4) изображена на рис. 4.3.1.
Теперь полагаем, что для настройки регулятора в составе обобщенного настраиваемого объекта используется не вектор состояния, а переменные на его выходе, образующие вектор  . Желаемые переменные
. Желаемые переменные  определяются уравнением эталонной модели и обозначаются как
определяются уравнением эталонной модели и обозначаются как  . Функционал
. Функционал  выберем квадратичным с аргументом
выберем квадратичным с аргументом  :
:
 (4.3.5)
(4.3.5)
где матрица весовых коэффициентов  задается.
задается.
Тогда можно записать:
 .
.
Алгоритм скоростного градиента для вычисления параметров настройки  обобщенного настраиваемого объекта, заданного уравнениями типа (4.3.1) с желаемой динамикой изменения выходов и целью адаптации (2.3.5) приобретает следующий вид:
обобщенного настраиваемого объекта, заданного уравнениями типа (4.3.1) с желаемой динамикой изменения выходов и целью адаптации (2.3.5) приобретает следующий вид:
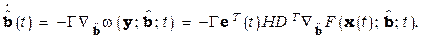
(4.3.6)
Для линейного нестационарного оператора 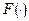 в уравнении обобщенного настраиваемого объекта (1):
в уравнении обобщенного настраиваемого объекта (1):
 (4.3.7)
(4.3.7)
где  ― параметрическое управление со стороны блока алгоритмов адаптации, имеем:
― параметрическое управление со стороны блока алгоритмов адаптации, имеем:
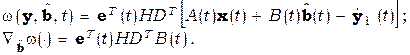
Тогда алгоритм скоростного градиента в т.н. дифференциальной форме для линейного нестационарного обобщенного настраиваемого объекта принимает вид:
 (4.3.8)
(4.3.8)
В (8)  ― ошибка адаптации;
― ошибка адаптации; 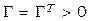 .
.
Наряду с алгоритмами СГ в дифференциальной форме могут применяться разнообразные модификации алгоритма СГ. При выполнении проекта рекомендуется исследовать моделируемую адаптивную систему с использованием модификации алгоритма СГ (4.3.4) в т.н. конечной форме:
 , (4.3.9)
, (4.3.9)
где  ― начальное значение вычисляемого параметра
― начальное значение вычисляемого параметра  . Заметим, что если вектор-функция
. Заметим, что если вектор-функция  удовлетворяет т.н. условию псевдоградиентности
удовлетворяет т.н. условию псевдоградиентности  , то алгоритмы типа (9) называют алгоритмами скоростного псевдоградиента. Эти алгоритмы есть уравнения относительно
, то алгоритмы типа (9) называют алгоритмами скоростного псевдоградиента. Эти алгоритмы есть уравнения относительно 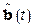 . Тогда, очевидно, алгоритмы скоростного градиента в упрощенной конечной форме применимы, если они разрешимы относительно искомого решения
. Тогда, очевидно, алгоритмы скоростного градиента в упрощенной конечной форме применимы, если они разрешимы относительно искомого решения 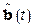 . Показано, что для этого достаточно, чтобы функция
. Показано, что для этого достаточно, чтобы функция  не зависела явно от искомого решения
не зависела явно от искомого решения 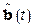 или удовлетворяла условию Липшица:
или удовлетворяла условию Липшица:
 при
при  .
.
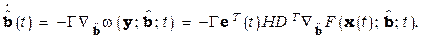 (4.3.6)
(4.3.6)

 , (4.3.1)
, (4.3.1) ― гладкая функция своих аргументов, линейно зависимая от настраиваемых параметров
― гладкая функция своих аргументов, линейно зависимая от настраиваемых параметров 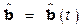 . Локальныйнеотрицательный функционал настройки
. Локальныйнеотрицательный функционал настройки  явно зависит от фазовых координат
явно зависит от фазовых координат  и не зависит явно от настраиваемых параметров
и не зависит явно от настраиваемых параметров  . Полная производная по времени
. Полная производная по времени  вычисляется очевидным образом с учетом уравнения (4.3.1):
вычисляется очевидным образом с учетом уравнения (4.3.1): (4.3.2)
(4.3.2) явно от времени не зависит. Тогда градиент
явно от времени не зависит. Тогда градиент  по настраиваемым параметрам
по настраиваемым параметрам  принимает вид:
принимает вид: (4.3.3)
(4.3.3)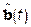 , в соответствии с дифференциальным уравнением первого порядка – алгоритмом градиентного метода:
, в соответствии с дифференциальным уравнением первого порядка – алгоритмом градиентного метода: (4.3.4)
(4.3.4) , получаем алгоритм СГ с интегральным оператором
, получаем алгоритм СГ с интегральным оператором 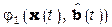 . Структура обобщенного настраиваемого объекта с алгоритмом управления
. Структура обобщенного настраиваемого объекта с алгоритмом управления  (4.3.4) изображена на рис. 4.3.1.
(4.3.4) изображена на рис. 4.3.1. . Желаемые переменные
. Желаемые переменные  определяются уравнением эталонной модели и обозначаются как
определяются уравнением эталонной модели и обозначаются как  . Функционал
. Функционал  выберем квадратичным с аргументом
выберем квадратичным с аргументом  :
: (4.3.5)
(4.3.5) задается.
задается. .
.
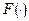 в уравнении обобщенного настраиваемого объекта (1):
в уравнении обобщенного настраиваемого объекта (1): (4.3.7)
(4.3.7) ― параметрическое управление со стороны блока алгоритмов адаптации, имеем:
― параметрическое управление со стороны блока алгоритмов адаптации, имеем: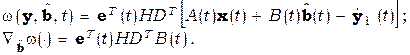
 (4.3.8)
(4.3.8) ― ошибка адаптации;
― ошибка адаптации; 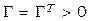 .
. , (4.3.9)
, (4.3.9) ― начальное значение вычисляемого параметра
― начальное значение вычисляемого параметра  . Заметим, что если вектор-функция
. Заметим, что если вектор-функция  удовлетворяет т.н. условию псевдоградиентности
удовлетворяет т.н. условию псевдоградиентности  , то алгоритмы типа (9) называют алгоритмами скоростного псевдоградиента. Эти алгоритмы есть уравнения относительно
, то алгоритмы типа (9) называют алгоритмами скоростного псевдоградиента. Эти алгоритмы есть уравнения относительно 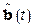 . Тогда, очевидно, алгоритмы скоростного градиента в упрощенной конечной форме применимы, если они разрешимы относительно искомого решения
. Тогда, очевидно, алгоритмы скоростного градиента в упрощенной конечной форме применимы, если они разрешимы относительно искомого решения  не зависела явно от искомого решения
не зависела явно от искомого решения  при
при  .
.


