Дискретные адаптивные системы с неявной эталонной моделью
Методика синтеза дискретных адаптивных систем с неявной эталонной моделью, предназначенных для решения наиболее общей задачи управления – задачи слежения с заданной динамикой, аналогична методике синтеза непрерывной адаптивной системы с градиентным алгоритмом адаптации. Пусть математическая модель объекта задана в виде линейного разностного уравнения:
где
- гурвицевы полиномы, т. е. линейный объект является минимально-фазовым, Эталонную модель зададим уравнением вход-выход:
где полиномы
— гурвицевы, коэффициенты Целевые условия запишем в виде предельного равенства:
Введём обобщённую ошибку:
Если из (5.4.1) вычесть (5.4.2) и добавить к обеим частям
Уравнение (5.4.5) можно записать в векторной форме:
где «идеальный» при Таким образом, закон регулирования Целевое условие адаптации и управления целесообразно выбирать в виде квадратичной функции
где вектор Если нет гипотез о статистической природе измерений
где число
Работоспособность алгоритма (5.4.7), (5.4.8), т. е. сходимость при
|

 (5.4.1)
(5.4.1)

 - неизмеряемая помеха, но ограниченная по уровню
- неизмеряемая помеха, но ограниченная по уровню  .
. (5.4.2)
(5.4.2)

 ,
,  известны.
известны. (5.4.3)
(5.4.3) . (5.4.4)
. (5.4.4) то, учитывая, что
то, учитывая, что  , получим «идеальный» дискретный закон управления:
, получим «идеальный» дискретный закон управления: (5.4.5)
(5.4.5) , (5.4.6)
, (5.4.6) вектор параметров регулятора основного контура
вектор параметров регулятора основного контура  с размерностью N=n+2(m+1);
с размерностью N=n+2(m+1);  — вектор измеряемых значений решётчатых функций.
— вектор измеряемых значений решётчатых функций. в виде (5.4.5) и (5.4.6) линеен по параметрам
в виде (5.4.5) и (5.4.6) линеен по параметрам  . Вектор
. Вектор  содержит ненастраиваемую компоненту
содержит ненастраиваемую компоненту 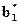 — стационарная часть адаптивного регулятора и настраиваемую – вектор
— стационарная часть адаптивного регулятора и настраиваемую – вектор  в соответствии с алгоритмом и целевым условием адаптации. Регулятор «идеален» в смысле достигаемой цели управления (5.4.3), если все
в соответствии с алгоритмом и целевым условием адаптации. Регулятор «идеален» в смысле достигаемой цели управления (5.4.3), если все  ,
,  .
.
 — вектор текущих и неизмеряемых параметров модели объекта.
— вектор текущих и неизмеряемых параметров модели объекта. , то алгоритмом адаптации может быть детерминированный градиентный алгоритм с ограничением на шаг адаптации
, то алгоритмом адаптации может быть детерминированный градиентный алгоритм с ограничением на шаг адаптации  :
: ,
,  (5.4.7)
(5.4.7) — верхняя оценка неизвестного коэффициента
— верхняя оценка неизвестного коэффициента  ; тогда
; тогда (5.4.8)
(5.4.8) , показывается методом Ляпунова, где функцией Ляпунова в данном случае является квадрат параметрического рассогласования:
, показывается методом Ляпунова, где функцией Ляпунова в данном случае является квадрат параметрического рассогласования:  . Из условия
. Из условия  следует условие сходимости в виде (5.4.8).
следует условие сходимости в виде (5.4.8).


