Для вычисления вектора настраиваемых параметров 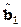 согласно уравнению (6) АА использует значения
согласно уравнению (6) АА использует значения  и
и  , а в качестве целевой функции
, а в качестве целевой функции  ― квадратичный функционал с аргументом, однозначно соответствующим мгновенным значениям параметрических рассогласований
― квадратичный функционал с аргументом, однозначно соответствующим мгновенным значениям параметрических рассогласований  для
для  и
и 
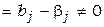 для
для  . В качестве такого аргумента целесообразно выбрать обобщенную ошибку адаптивного управления:
. В качестве такого аргумента целесообразно выбрать обобщенную ошибку адаптивного управления:
 (3.2.8)
(3.2.8)
или, как это можно показать, равносильную ей функцию
 (3.2.9)
(3.2.9)
В исследуемой системе примем
 (3.2.10)
(3.2.10)
В соответствие с градиентным методом отыскания  алгоритм адаптации, точнее, алгоритм вычисления вектора настраиваемых параметров
алгоритм адаптации, точнее, алгоритм вычисления вектора настраиваемых параметров 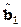 в составе вектора
в составе вектора  имеет вид:
имеет вид:
 (3.2.11)
(3.2.11)
где  матрица размерностью
матрица размерностью  .
.
Введем вектор измерений  и вектор
и вектор  . Тогда (напомним, что ранее было принято
. Тогда (напомним, что ранее было принято 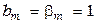 ) вместо (8) можно записать для обобщенной ошибки
) вместо (8) можно записать для обобщенной ошибки  равносильное соотношение:
равносильное соотношение:
 (3.2.12)
(3.2.12)
Здесь наиболее ярко проявилась зависимость аргумента 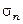 целевой функции
целевой функции  от мгновенных отклонений вычисляемых по алгоритму (3.2.11) текущих значений параметров регулятора
от мгновенных отклонений вычисляемых по алгоритму (3.2.11) текущих значений параметров регулятора  от их истинных значений
от их истинных значений  . С учетом (3.2.12) алгоритм адаптации примет вид:
. С учетом (3.2.12) алгоритм адаптации примет вид:
 (3.2.13)
(3.2.13)
 и
и  ― начальные условия вычислительной процедуры (3.2.13) заданы. Скалярная функция
― начальные условия вычислительной процедуры (3.2.13) заданы. Скалярная функция  в (3.2.13) вычисляется согласно выражению (3.2.9), которое в этом случае можно записать следующим образом:
в (3.2.13) вычисляется согласно выражению (3.2.9), которое в этом случае можно записать следующим образом:
 (3.2.14)
(3.2.14)
где:

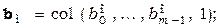
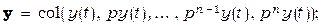

Как видно из алгоритма адаптации (3.2.13) и (3.2.14), в правой части (3.2.13) отсутствует ошибка  , а неявная эталонная модель задается коэффициентами
, а неявная эталонная модель задается коэффициентами  для вычислений
для вычислений  . Цель управления и одновременно цель адаптации достигается при
. Цель управления и одновременно цель адаптации достигается при  тогда, когда
тогда, когда  , т.е. движение в системе соответствуют уравнению модели (3.2.2). При этом параметрические рассогласования
, т.е. движение в системе соответствуют уравнению модели (3.2.2). При этом параметрические рассогласования  ,
,  обращаются в нуль и система становится стационарной. Процессы
обращаются в нуль и система становится стационарной. Процессы  и
и  целесообразно уменьшать надлежащим выбором матрицы
целесообразно уменьшать надлежащим выбором матрицы  при выбранном функционале
при выбранном функционале  . Здесь важно уяснить, что алгоритм (3.2.13) сходится (или не сходится) не только в зависимости от выбранного
. Здесь важно уяснить, что алгоритм (3.2.13) сходится (или не сходится) не только в зависимости от выбранного  , но и от
, но и от  , где
, где  ― вектор неизвестных параметров математической модели объекта управления (3.2.1):
― вектор неизвестных параметров математической модели объекта управления (3.2.1): 
 . Исследование условий сходимости алгоритмов адаптации может быть осуществлено методом функций Ляпунова (аналитическое решение задачи) или ― при
. Исследование условий сходимости алгоритмов адаптации может быть осуществлено методом функций Ляпунова (аналитическое решение задачи) или ― при
компьютерном моделировании ― эвристическим путем.
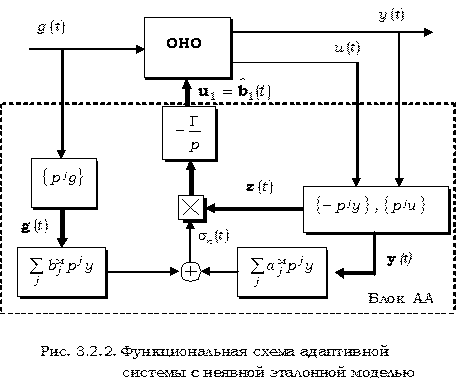
Функциональная схема адаптивной системы с неявной эталонной моделью и градиентным непрерывным алгоритмом адаптации, составленная по уравнениям и алгоритмам (3.2.1) ― (3.2.3), (3.2.6), (3.2.13), (3.2.14), изображена на рис. 3.2.2 и служит основой для составления схемы компьютерного моделирования с использованием пакета MATLAB®.

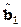 согласно уравнению (6) АА использует значения
согласно уравнению (6) АА использует значения  и
и  , а в качестве целевой функции
, а в качестве целевой функции  ― квадратичный функционал с аргументом, однозначно соответствующим мгновенным значениям параметрических рассогласований
― квадратичный функционал с аргументом, однозначно соответствующим мгновенным значениям параметрических рассогласований  для
для  и
и 
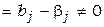 для
для  . В качестве такого аргумента целесообразно выбрать обобщенную ошибку адаптивного управления:
. В качестве такого аргумента целесообразно выбрать обобщенную ошибку адаптивного управления: (3.2.8)
(3.2.8) (3.2.9)
(3.2.9) (3.2.10)
(3.2.10) алгоритм адаптации, точнее, алгоритм вычисления вектора настраиваемых параметров
алгоритм адаптации, точнее, алгоритм вычисления вектора настраиваемых параметров  имеет вид:
имеет вид: (3.2.11)
(3.2.11) матрица размерностью
матрица размерностью  .
. и вектор
и вектор  . Тогда (напомним, что ранее было принято
. Тогда (напомним, что ранее было принято 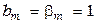 ) вместо (8) можно записать для обобщенной ошибки
) вместо (8) можно записать для обобщенной ошибки  равносильное соотношение:
равносильное соотношение: (3.2.12)
(3.2.12)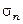 целевой функции
целевой функции  от их истинных значений
от их истинных значений  . С учетом (3.2.12) алгоритм адаптации примет вид:
. С учетом (3.2.12) алгоритм адаптации примет вид: (3.2.13)
(3.2.13) и
и  ― начальные условия вычислительной процедуры (3.2.13) заданы. Скалярная функция
― начальные условия вычислительной процедуры (3.2.13) заданы. Скалярная функция  (3.2.14)
(3.2.14)
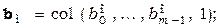
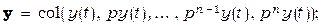

 , а неявная эталонная модель задается коэффициентами
, а неявная эталонная модель задается коэффициентами  для вычислений
для вычислений  тогда, когда
тогда, когда  , т.е. движение в системе соответствуют уравнению модели (3.2.2). При этом параметрические рассогласования
, т.е. движение в системе соответствуют уравнению модели (3.2.2). При этом параметрические рассогласования  ,
,  обращаются в нуль и система становится стационарной. Процессы
обращаются в нуль и система становится стационарной. Процессы  и
и  целесообразно уменьшать надлежащим выбором матрицы
целесообразно уменьшать надлежащим выбором матрицы  при выбранном функционале
при выбранном функционале  , где
, где  ― вектор неизвестных параметров математической модели объекта управления (3.2.1):
― вектор неизвестных параметров математической модели объекта управления (3.2.1): 
 . Исследование условий сходимости алгоритмов адаптации может быть осуществлено методом функций Ляпунова (аналитическое решение задачи) или ― при
. Исследование условий сходимости алгоритмов адаптации может быть осуществлено методом функций Ляпунова (аналитическое решение задачи) или ― при