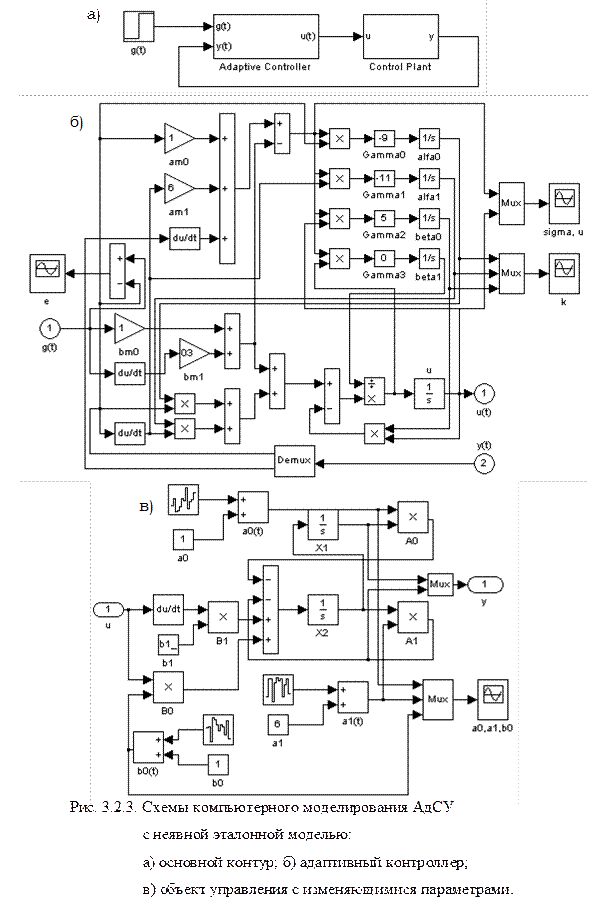
В качестве прототипа исследуемой в проекте темы рассмотрим решение задачи синтеза адаптивной системы с неявной эталонной моделью основного контура. Основной контур (рис. 3.2.1, а) содержит линейный объект управления второго порядка с изменяющимися коэффициентами:

Значения коэффициентов уравнения объекта заданы в диапазоне возможных значений 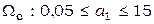 ;
;  ;
;  ;
;  . Переменные
. Переменные 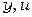 измеряются. Эталонная модель устойчивой и минимально-фазовой системы управления задана уравнением
измеряются. Эталонная модель устойчивой и минимально-фазовой системы управления задана уравнением
 ,
,
где все коэффициенты >0 и принадлежат множеству  .
.
Цель адаптивного управления — достижение предельного равенства  при воспроизведении входного воздействия
при воспроизведении входного воздействия  Для этого “идеальный” закон регулирования должен удовлетворять уравнению (3.2.6):
Для этого “идеальный” закон регулирования должен удовлетворять уравнению (3.2.6):
 .
.
Если бы параметры уравнения объекта были бы известными, то легко удостовериться, что выбором параметров “идеального” регулятора 
 цель управления достигается и ошибка
цель управления достигается и ошибка  .
.
Для случаев, когда текущие значения параметров  неизвестны, параметры уравнения “идеального” регулятора вычисляются в реальном времени, для чего используются текущие измерительные данные
неизвестны, параметры уравнения “идеального” регулятора вычисляются в реальном времени, для чего используются текущие измерительные данные  и алгоритмы адаптации (3.2.11). Для квадратичного функционала настройки параметров
и алгоритмы адаптации (3.2.11). Для квадратичного функционала настройки параметров  обобщенная ошибка адаптивного управления
обобщенная ошибка адаптивного управления 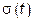 вычисляется по формуле (3.2.9):
вычисляется по формуле (3.2.9):
 .
.
Очевидно, что для вычисления ошибки 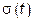 необходимо не только измерение сигналов
необходимо не только измерение сигналов  , но и вычисление их производных по времени
, но и вычисление их производных по времени 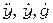 .
.
Согласно общему алгоритму (3.2.11) настройка параметров “идеального” закона регулирования  , где
, где 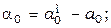
 ;
;  , в данном примере осуществляется по алгоритму
, в данном примере осуществляется по алгоритму
 ,
,
где вычисляется вектор-столбец  . Для этого следует использовать обобщенную ошибку
. Для этого следует использовать обобщенную ошибку 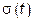 в виде (3.2.12), где эта ошибка явно зависит от настраиваемых параметров
в виде (3.2.12), где эта ошибка явно зависит от настраиваемых параметров  . Для квадратичного функционала настройки вектор-столбец
. Для квадратичного функционала настройки вектор-столбец 
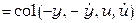 . Тогда алгоритм настройки параметров “идеального” адаптивного регулятора распадается на три (в данном примере) билинейных алгоритма:
. Тогда алгоритм настройки параметров “идеального” адаптивного регулятора распадается на три (в данном примере) билинейных алгоритма:
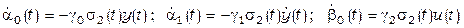 .
.
Из анализа функции Ляпунова для подобных задач следует, что полученные билинейные алгоритмы сходятся при любых значениях  . Величина шага
. Величина шага  сказывается на скорости и качестве процессов настройки параметров.
сказывается на скорости и качестве процессов настройки параметров.
Функциональная схема адаптивной системы в рассматриваемом примере следует из общей схемы, приведенной на рис. 3. В проекте необходимо составить самостоятельно схему в соответствии с расчетными соотношениями.
Отметим, что можно упростить систему, если обобщенную ошибку вычислять не как ошибку  , где индекс указывает на порядок высшей используемой производной сигнала невязки
, где индекс указывает на порядок высшей используемой производной сигнала невязки  в составе
в составе  , а с использованием только первой производной невязки
, а с использованием только первой производной невязки  . Тогда обобщенная ошибка адаптивного управления примет вид
. Тогда обобщенная ошибка адаптивного управления примет вид  . Однако при таком упрощении нарушается достаточное условие асимптотической устойчивости по Ляпунову и сходимость алгоритмов адаптации, полученных выше, уже не обеспечивается при любых значениях
. Однако при таком упрощении нарушается достаточное условие асимптотической устойчивости по Ляпунову и сходимость алгоритмов адаптации, полученных выше, уже не обеспечивается при любых значениях  . Но это уже самостоятельная задача анализа условий работоспособности АдСУ.
. Но это уже самостоятельная задача анализа условий работоспособности АдСУ.
Схема компьютерного моделирования с использованием пакета MATLAB® показана на рис. 3.2.3. Параметры адаптивной системы приведены на схемах. Параметры  и
и  изменяются скачком периодически (в приведенном примере с различными периодами для различных параметров от 10 до 30 с) на случайное значение в заданных пределах; параметр
изменяются скачком периодически (в приведенном примере с различными периодами для различных параметров от 10 до 30 с) на случайное значение в заданных пределах; параметр  . Адаптивный регулятор (adaptive controller на рис. 3.2.3, а, б) формирует параметрические управляющие воздействия
. Адаптивный регулятор (adaptive controller на рис. 3.2.3, а, б) формирует параметрические управляющие воздействия  .
.
Содержание отчета
1. Структурная схема системы управления. 2) Результаты моделирования.


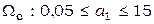 ;
;  ;
;  ;
;  . Переменные
. Переменные 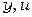 измеряются. Эталонная модель устойчивой и минимально-фазовой системы управления задана уравнением
измеряются. Эталонная модель устойчивой и минимально-фазовой системы управления задана уравнением ,
, .
. при воспроизведении входного воздействия
при воспроизведении входного воздействия  Для этого “идеальный” закон регулирования должен удовлетворять уравнению (3.2.6):
Для этого “идеальный” закон регулирования должен удовлетворять уравнению (3.2.6): .
.
 цель управления достигается и ошибка
цель управления достигается и ошибка  .
. неизвестны, параметры уравнения “идеального” регулятора вычисляются в реальном времени, для чего используются текущие измерительные данные
неизвестны, параметры уравнения “идеального” регулятора вычисляются в реальном времени, для чего используются текущие измерительные данные  и алгоритмы адаптации (3.2.11). Для квадратичного функционала настройки параметров
и алгоритмы адаптации (3.2.11). Для квадратичного функционала настройки параметров  обобщенная ошибка адаптивного управления
обобщенная ошибка адаптивного управления 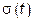 вычисляется по формуле (3.2.9):
вычисляется по формуле (3.2.9): .
.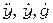 .
. , где
, где 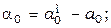
 , в данном примере осуществляется по алгоритму
, в данном примере осуществляется по алгоритму ,
, . Для этого следует использовать обобщенную ошибку
. Для этого следует использовать обобщенную ошибку 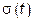 в виде (3.2.12), где эта ошибка явно зависит от настраиваемых параметров
в виде (3.2.12), где эта ошибка явно зависит от настраиваемых параметров  . Для квадратичного функционала настройки вектор-столбец
. Для квадратичного функционала настройки вектор-столбец 
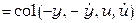 . Тогда алгоритм настройки параметров “идеального” адаптивного регулятора распадается на три (в данном примере) билинейных алгоритма:
. Тогда алгоритм настройки параметров “идеального” адаптивного регулятора распадается на три (в данном примере) билинейных алгоритма: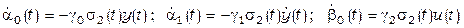 .
. . Величина шага
. Величина шага  сказывается на скорости и качестве процессов настройки параметров.
сказывается на скорости и качестве процессов настройки параметров. , где индекс указывает на порядок высшей используемой производной сигнала невязки
, где индекс указывает на порядок высшей используемой производной сигнала невязки  в составе
в составе  , а с использованием только первой производной невязки
, а с использованием только первой производной невязки  . Тогда обобщенная ошибка адаптивного управления примет вид
. Тогда обобщенная ошибка адаптивного управления примет вид  . Однако при таком упрощении нарушается достаточное условие асимптотической устойчивости по Ляпунову и сходимость алгоритмов адаптации, полученных выше, уже не обеспечивается при любых значениях
. Однако при таком упрощении нарушается достаточное условие асимптотической устойчивости по Ляпунову и сходимость алгоритмов адаптации, полученных выше, уже не обеспечивается при любых значениях  . Но это уже самостоятельная задача анализа условий работоспособности АдСУ.
. Но это уже самостоятельная задача анализа условий работоспособности АдСУ. и
и  изменяются скачком периодически (в приведенном примере с различными периодами для различных параметров от 10 до 30 с) на случайное значение в заданных пределах; параметр
изменяются скачком периодически (в приведенном примере с различными периодами для различных параметров от 10 до 30 с) на случайное значение в заданных пределах; параметр  . Адаптивный регулятор (adaptive controller на рис. 3.2.3, а, б) формирует параметрические управляющие воздействия
. Адаптивный регулятор (adaptive controller на рис. 3.2.3, а, б) формирует параметрические управляющие воздействия  .
.