ПРИМЕР 5. K = 100, п = 5, i = 10% годовых, ежегодный прирост платежей на 15%, k = 0,15.
K = 100, п = 5, i = 10% годовых, ежегодный прирост платежей на 15%, k = 0,15. Коэффициент рассрочки находится по формуле (7.18):
На момент окончания первого года получим: R 1 = 100 х 0,20089 = 20,089; D 1 x i = 100 х 0,1 = 10,0; d 1 = 20,089 -10,0 = 10,089. Далее последовательно находим Rt, Dt, dt. Причем Rt = 20,089 x 1,15 t -1.
Если предусматривается систематическое сокращение размеров платежей, например k = -15%, то R 1 = 34,507. Rt = 34,507 х (1 - 0,15) t -1. Регулярные постоянные платежи (метод Б) Напомним, что согласно этой схеме величина периодических лизинговых платежей определяется как сумма погашения основного долга (амортизация стоимости оборудования) и выплат процентов. Размер амортизации может быть определен с помощью различных методов (см. гл. 2 "Модели износа оборудования"). Далее рассматривается только линейная модель амортизации, поскольку этот метод является преобладающим в отечественной практике. Согласно этой модели сумма амортизационного отчисления d определяется "бухгалтерским" способом по соответствующим нормативам или иным путем. Так или иначе, но расчет выполняется по схеме погашения задолженности равными долями (суммами)[40].При погашении всей первоначальной стоимости
при частичном возмещении стоимости
Платежи по лизингу в конце периода t находятся как Rt = Dt - 1 x i + d, (7.19) где Rt — размер лизингового платежа в периоде t. Остаток долга на конец периода находится последовательно: Dt = Dt - 1 - d (7.20) или
|

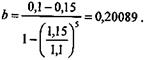
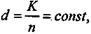
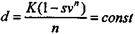 .
. .
.


