МЕТОДИКА Б. Прогноз суммы показателей
Рассматриваются два варианта постановки задачи, когда слагаемые — это независимые величины и когда они зависимы друг от друга[45]. Независимые слагаемые. Прогнозируемый показатель представляет собой сумму некоторых однородных величин. Слагаемые — независимые или слабо зависимые между собой показатели. Определение прогнозного интервала предполагает выполнение следующих последовательных шагов: • установление РВД и определение видов распределений (напомним, что все они симметричные); • расчет средних значений этих распределений и дисперсий; • расчет общей средней (суммы частных средних) и дисперсии суммы; • оценка границ интервального прогноза. Формулы для расчета средних и дисперсий приведены в табл. 8.3 [46]. Таблица 8.3
Во всех приведенных в таблице формулах L = b - a. Расчет суммы средних и дисперсии суммы производится следующим образом: • сумма частных средних
• дисперсия суммы
где Мj, Dj — средние значения и дисперсии частных распределений; • стандартная ошибка
Интервал прогноза определяется как
где z (нормированное отклонение) находится по табл. 8.2 или табл. 5 Приложения в зависимости от принятой ДВ.
|

 ; (8.10)
; (8.10) , (8.11)
, (8.11)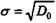 . (8.12)
. (8.12) , (8.13)
, (8.13)


