ПРИМЕР 3. Используем данные примера 2 и найдем интервальный прогноз для суммы теперь уже зависимых слагаемых при условии
Используем данные примера 2 и найдем интервальный прогноз для суммы теперь уже зависимых слагаемых при условии, что коэффициенты корреляции неизвестны. Примем, что ДВ для суммы равна 75%. Соответственно для отдельного слагаемого ДВ j =
МЕТОДИКА В. Прогноз произведения двух параметров Иногда прогнозируемый показатель представляет собой произведение двух величин Y = VW, где одна величина — качественная характеристика (производительность труда, фондоотдача и т. п.), вторая — объемная величина (количество отработанного времени, размер фондов и пр.). Показатель Y прогнозируется не непосредственно, а на основе прогнозов сомножителей. Если рассматривать сомножители как независимые величины (а в большинстве случаев это правомерно), то методика сводится к следующему. 1. Для каждого сомножителя находится интервальный прогноз: V 1, V 2; W 1, W 2.При этом доверительная вероятность принимается на уровне P. Причем
Иначе говоря, прогноз сомножителей должен быть сделан с большей доверительной вероятностью, чем прогноз итогового показателя (см. табл. 8.4; в ней же приводятся соответствующие значения Таблица 8.4
2. Рассчитываются граничные значения прогнозного интервала как произведения V 1 W 1, V 2 W 2.С вероятностью ДВ можно утверждать, что реальное значение Y будет находиться в указанных пределах. Можно применить и иной подход, взяв за базу средние распределений. Тогда последовательно находим: средние и дисперсии каждого распределения, произведение средних и дисперсию произведения. Последняя рассчитывается следующим образом[47]:
где Dj и Mj — дисперсия и средняя.
|

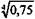 = 0,93. По формуле (8.1) находим
= 0,93. По формуле (8.1) находим 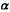 = 0,035. Результаты расчетов величин x, vj и wj представлены в следующей таблице.
= 0,035. Результаты расчетов величин x, vj и wj представлены в следующей таблице.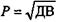 .
.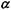 ).
).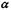
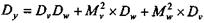 , (8.15)
, (8.15)


