ПРИМЕР 2. Эксперты установили следующие РВД и виды распределений для четырех слагаемых (в целях иллюстрации метода приняты различные виды распределений):
Эксперты установили следующие РВД и виды распределений для четырех слагаемых (в целях иллюстрации метода приняты различные виды распределений):
Полученные по этим данным значения частных средних и дисперсий приведены в следующей таблице.
Пусть доверительная вероятность равна 75%, F (z) = 0,75. По табл. 8.2 находим z = 1,15; в свою очередь, получим Нижняя и верхняя границы прогнозного интервала равны: A = 96 - 1,15 x 2 = 93,7; B = 96 + 1,15 x 2 = 98,3. Как видим, интервал прогноза заметно уже, чем суммы граничных значений РВД слагаемых (88 — 104), но вероятность "попадания" в него также меньше (не 100, а 75%). Сильная зависимость между слагаемыми. Теоретически обоснованное решение проблемы требует в этой ситуации измерения коэффициентов корреляции между попарно взятыми случайными переменными (в нашем случае — слагаемыми). Поскольку следует ожидать в основном положительной корреляции, то дисперсия увеличивается. Следовательно, увеличивается и интервал прогноза. Например, если в примере 2 полагать, что коэффициенты корреляции у всех пар слагаемых одинаковы и равны, допустим, 0,9 (сильная положительная корреляция), то стандартная ошибка увеличится почти в 2 раза и составит 3,91 вместо 2. Искомый интервал в этом случае равен 91,5—100,5. Однако в такого рода задачах вряд ли практически возможен расчет коэффициентов корреляции (хотя бы в связи с отсутствием необходимой информации), поэтому целесообразно поступить иным образом, избежав тем самым расчет упомянутых коэффициентов. Для решения задачи определим граничные значения прогнозных интервалов для каждого слагаемого, применив методику А. Обозначим эти величины как Aj и Bj. Искомые граничные значения для суммы составят:
Слагаемые этих сумм рассчитаем с учетом того, что вероятности реализации прогноза для каждого слагаемого должны быть больше доверительной вероятности для суммы в целом. ДВ для суммы составит
Для отдельного слагаемого ДВ определяется как
|

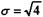 = 2.
= 2.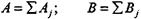 .
. .
.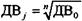 . (8.14)
. (8.14)


