Средняя арифметическая скорость
Относительная скорость применяется для расчета числа молекул, движущихся со скоростями в интервале от v до v + dv: u = v/vв. (2.20) Закон распределения молекул идеального газа по скоростям в стационарном состоянии (распределение Максвелла):
где dnv - среднее число молекул в единице объема со скоростями в интервале от v до v + dv; n - число молекул в единице объема. Функция распределения (доля молекул от их общего числа отнесена к некоторому интервалу скоростей):
где dnv/ndv - функция распределения. Свободные пробеги молекул - прямолинейные участки траектории, проходимые молекулой между двумя последовательными соударениями. Средняя длина свободного пробега молекулы – среднее расстояние, проходимое молекулой между двумя соударениями:
где Z - число соударений; < v> - средняя скорость молекулы; k - постоянная Больцмана; < d> - диаметр молекулы; p - давление; T - абсолютная температура. Среднее число соударений - число соударений молекул < Z>, численно равное отношению средней скорости движения молекул < v> к средней длине свободного пробега:
Эффективный диаметр молекулы d - минимальное расстояние, на которое сближаются при столкновении центры 2-х молекул. Эффективное сечение - величина равная s = pd2. (2.25) Барометрическая формула показывает, что давление убывает с высотой тем быстрее, чем тяжелее газ и чем ниже его температура:
Закон распределения молекул газа по высоте в поле сил тяготения (распределение Больцмана):
где no - число молекул в единице объема в том месте, где потенциальная энергия молекул равна нулю; n - число молекул в единице объема в тех точках пространства, где потенциальная энергия молекул равна Wp. Распределение Максвелла-Больцмана - благодаря этому распределению можно определить долю молекул идеального газа, имеющих скорости в интервале от v до v + dv и обладающих потенциалом c = gh во внешнем силовом поле:
где vв - наиболее вероятная скорость, значению которой соответствует максимум кривой Максвелла. Зависимость плотности газа от высоты:
где mo - масса одной молекулы. 2.3. Основные положения и законы термодинамики Первое начало термодинамики - закон сохранения и превращения энергии, которым сопровождаются термодинамические процессы – количество тепла, подводимого к системе, идет на изменение ее внутренней энергии и работу, производимую системой против внешних сил:
где dU - изменение внутренней энергии системы; dQ - элементарное количество тепла, подводимого к системе; dA - элементарная работа, совершаемая системой. Изотермический процесс - процесс, протекающий при постоянной температуре (T = const). При изотермическом процессе все подводимое к системе тепло идет на совершение этой системой работы а U = = const. Работа, совершаемая произвольной массой m идеального газа при изотермическом процессе:
Изобарический процесс – процесс, протекающий при постоянном давлении (p = const). При этом подводимое к системе тепло идет как на изменение ее внутренней энергии, так и на совершение этой системой работы:
Работа, совершаемая произвольной массой m идеального газа при изобарическом процессе:
Изменение внутренней энергии произвольной массы m идеального газа при изобарическом процессе:
Изохорический процесс – процесс, протекающий при постоянном объеме (V = const). При этом все подводимое к системе тепло идет на изменение ее внутренней энергии:
Адиабатический процесс - процесс, протекающий без теплообмена или почти без теплообмена с окружающей средой. При этом работа может совершаться системой только за счет убыли ее внутренней энергии:
Уравнения адиабатического процесса (уравнения Пуассона):
Работа, совершаемая произвольной массой m идеального газа при адиабатическом расширении:
Политропический процесс - такой процесс, при котором p и V связаны соотношением:
где n - показатель политропы, принимающий любые значения от - ¥ до + ¥. В частности для изобарического процесса n = 0, изотермического - n = 1, адиабатического - n = g, изохорического - n = ¥. Работа, совершаемая произвольной массой m идеального газа при политропическом процессе:
Работа, совершаемая идеальным газом при круговом процессе, равна разности работ при расширении А1 и при сжатии А2 газа и эквивалентна разности количеств тепла, подводимого к системе при расширении Q1 и отводимого от нее при сжатии Q2:
Коэффициент полезного действия кругового процесса (цикла) - физическая величина, равная отношению работы цикла к работе, которую можно было бы совершить при превращении в нее всего количества тепла, подведенного к системе:
Цикл Карно - цикл, состоящий из двух изотермических и двух адиабатических процессов. Работа, совершаемая произвольной массой m идеального газа в цикле Карно, - разность между работой, совершенной системой при расширении, и работой, совершенной над системой при ее сжатии:
Коэффициент полезного действия цикла Карно h не зависит от природы вещества, а зависит лишь от температур, при которых теплота сообщается системе и отбирается от нее:
Коэффициент полезного действия холодильной машины (холодильника):
Цикл Отто состоит из двух адиабат и двух изохор. Цикл Дизеля состоит из двух адиабат, изохоры и изобары. Энтропия - физическая величина, элементарное изменение которой при переходе системы из одного состояния в другое равно полученному или отданному количеству теплоты, деленному на температуру, при которой произошел этот процесс:
Связь энтропии системы с термодинамической вероятностью (соотношение Больцмана): S = k× ln w, (2.47) где k - постоянная Больцмана.
|

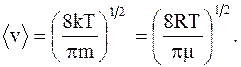 (2.19)
(2.19)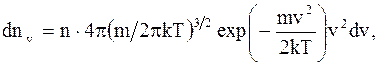 (2.21)
(2.21)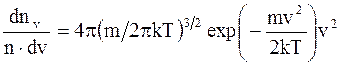 или
или 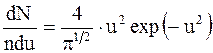 , (2.22)
, (2.22)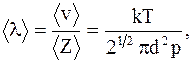 (2.23)
(2.23)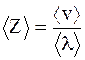 ,
, 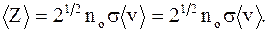 (2.24)
(2.24)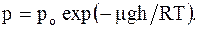 (2.26)
(2.26)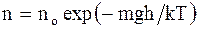 ,
, 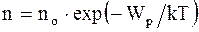 , (2.27)
, (2.27)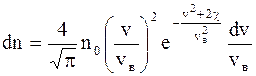 , (2.28)
, (2.28)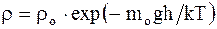 ;
; 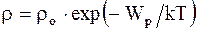 , (2.29)
, (2.29)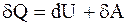 , (2.30)
, (2.30)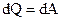 , при этом dU = CvdT = 0,
, при этом dU = CvdT = 0,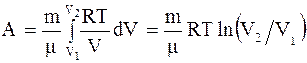 . (2.31)
. (2.31)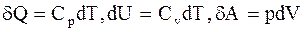 . (2.32)
. (2.32)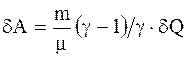 . (2.33)
. (2.33)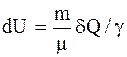 . (2.34)
. (2.34)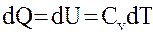 ,
, 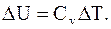 (2.35)
(2.35)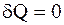 ,
, 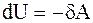 . (2.36)
. (2.36)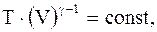
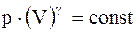 ;
; 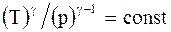 . (2.37)
. (2.37)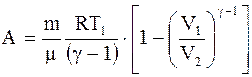 . (2.38)
. (2.38)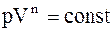 , (2.39)
, (2.39)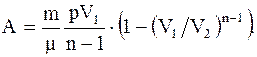 (2.40)
(2.40)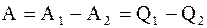 . (2.41)
. (2.41)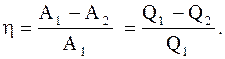 (2.42)
(2.42)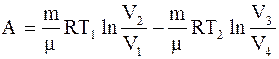 . (2.43)
. (2.43)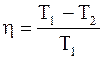 . (2.44)
. (2.44)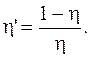 (2.45)
(2.45)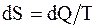 . (2.46)
. (2.46)


