Мгновенная мощность при вращательном движении
где M - мгновенный момент силы; ω - мгновенная угловая скорость. 1.4. Законы сохранения в механике Закон сохранения энергии в его общефизическом смысле - энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой, в количественном отношении оставаясь неизменной. Закон сохранения и превращения механической энергии - полная механическая энергия замкнутой системы (в отсутствие внешних воздействий), в которой действуют только консервативные силы, остается величиной постоянной: Wk + Wp = const. (1.114) Закон сохранения импульса - полный импульс замкнутой системы в отсутствии внешних воздействий остается величиной постоянной: p = const. (1.115) Закон движения центра масс - центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует равнодействующая всех внешних сил:
Импульс незамкнутой системы сохраняется, если геометрическая сумма всех внешних сил равна нулю. Удар - совокупность явлений, возникающих при столкновении движущихся твердых тел, а также при некоторых видах взаимодействия твердого тела с жидкостью или газом. Ударный импульс - мера механического взаимодействия тел при ударе ударной силы F за время удара τ:
Коэффициент восстановления k – величина, характеризующая потери энергии при ударе, численно равная отношению скорости взаимодействующих масс после взаимодействия к их скорости до взаимодействия:
Центральный удар – такой удар, при котором центры масс тел лежат на линии удара. Прямой центральный удар – такой, при котором скорости v1 и v2 центров масс в начале удара направлены параллельно линии удара. Центральный абсолютно неупругий удар шаров характеризуется тем, что выполняется только закон сохранения импульса. Скорость шаров после центрального абсолютно неупругого удара:
Центральный абсолютно упругий удар шаров характеризуется тем, что выполняются законы сохранения полной механической энергии и импульса. Скорости шаров после взаимодействия:
Закон сохранения момента импульса - момент импульса замкнутой системы в отсутствие внешних воздействий остается величиной постоянной:
Скорость изменения момента импульса (уравнение моментов):
где L0 - момент импульса тела (системы) относительно начала координат; Mвн - суммарный вращающий момент внешних сил, действующих на тело (систему). 1.5. Поле тяготения Поле тяготения создается взаимодействующими массами покоя тел и поэтому является характерным для тел с большими массами и со значениями скорости движения гораздо меньшими, чем скорость распространения света в вакууме. Напряженность поля тяготения - векторная физическая величина, равная по величине и направлению силе, действующей на единичную массу, помещенную в данную точку поля:
Ускорение, приобретаемое в поле тяготения массой m, направлено к центру большей массы:
Ускорение свободного падения вблизи поверхности Земли:
Ускорение силы тяжести при круговой траектории движения является центростремительным:
Потенциал поля тяготения - скалярная физическая величина, равная потенциальной энергии единичной массы, помещенной в данную точку поля:
Связь между напряженностью и потенциалом поля тяготения:
В векторной форме:
Знак “ – “означает, что напряженность поля тяготения направлена в сторону уменьшения потенциала поля тяготения. Уравнение движения массы m в поле тяготения при скорости движения тела v0< < с:
Первая космическая скорость
Вторая космическая скорость
Период обращения спутника, совершающего движение по круговой орбите:
“ Потенциальная яма ” - ограниченная область пространства, определяемая физической природой взаимодействия частиц. В этой области пространства потенциальная энергия частицы меньше, чем вне ее. Характеристики “потенциальной ямы”: а) ширина – расстояние, на котором проявляется действие сил притяжения; б) глубина – разность потенциальных энергий частицы на “краю” ямы и на ее “дне”, соответствующем минимуму потенциальной энергии, которую удобнее принять равной нулю. Основное свойство “потенциальной ямы” – способность удерживать частицу, полная энергия W которой меньше Потенциальный барьер – ограниченная в пространстве область, по обе стороны которой потенциальная энергия резко спадает. Прохождение частицы через потенциальный барьер возможно лишь в том случае, если ее полная энергия не меньше высоты потенциального барьера W³ 1.6. Волновые процессы Волны – изменения состояния среды (возмущения), распространяющиеся в этой среде и несущие с собой энергию - процесс распространения колебаний в пространстве. Фронт волны (волновой фронт) - геометрическое место точек, до которых доходят волны за некоторый промежуток времени t. Волновая поверхность - геометрическое место точек, колеблющихся в одинаковой фазе. Основное свойство волн, независимо от их природы, - перенос энергии без переноса вещества в пространстве. Упругие (или механические) волны - механические возмущения, возникающие и распространяющиеся в упругой среде. Различают продольные и поперечные волны. Продольные волны - волны, направление распространения которых совпадает с направлением смещения (колебания) частиц среды. Поперечные – волны, направление распространения которых и направление смещения (колебания) частиц среды взаимно перпендикулярны. В жидкостях и газах возникают и распространяются только продольные волны (“волны сжатия”). В твердых телах возникают и распространяются не только продольные, но и поперечные волны (“волны сдвига”). Одиночная волна (импульс) - сравнительно короткое возмущение, не имеющее регулярного характера. Волновой пакет – совокупность волн, частоты которых мало отличаются друг от друга. Бегущие волны - волны, которые переносят в пространстве энергию. Гармоническая волна – бесконечная синусоидальная волна, в которой все изменения среды происходят по закону синуса или косинуса. Плоские волны – такие, волновые поверхности которых представляют собой систему параллельных друг другу плоскостей, перпендикулярных направлению распространения волны. Сферические волны - такие, волновые поверхности которых представляют собой систему концентрических сферических поверхностей. Принцип суперпозиции волн - результат геометрического сложения когерентных волн. Когерентные волны – обладающие в каждой из точек среды постоянной разностью фаз и имеющие одинаковую частоту. Когерентные источники - точечные источники, размерами которых можно пренебречь, излучающие в пространство когерентные волны. Интерференция волн – явление наложения когерентных волн, в результате которого происходит перераспределение энергии волны в пространстве. Стоячая волна – волна, возникающая при интерференции двух встречных (падающей и отраженной) плоских волн с одинаковой амплитудой. Пучности стоячей волны - точки, в которых амплитуда удваивается. Узлы стоячей волны – точки, в которых амплитуда обращается в нуль. Длина стоячей волны - расстояние между соседними узлам l0:
Скорость распространения стоячей волны:
где L – некоторое расстояние, на котором наблюдается стоячая волна; n – число узлов; n - частота колебаний. Фазовая скорость упругих волн: продольных - где E – модуль Юнга; G – модуль сдвига. Групповая скорость - скорость перемещения в пространстве амплитуды волны:
Длина волны l - расстояние между ближайшими частицами, колеблющимися в одинаковой фазе (расстояние, на которое распространяется волна за один период):
где l - длина волны; T – период; n - частота; v – скорость распространения волны. Волновой вектор k определяет направление волны. Направление волнового вектора совпадает с направлением вектора скорости:
где w - круговая частота. Волновое число - численное значение волнового вектора:
Уравнение плоской прямой бегущей волны - выражение, которое определяет смещение колеблющейся точки как функцию ее координат и времени:
Уравнение плоской обратной бегущей волны:
Волновое уравнение плоской волны, распространяющейся вдоль оси X, дифференциальное уравнение второго порядка в частных производных:
Волновое уравнение плоской волны, распространяющейся в трехмерном пространстве:
где Уравнение стоячей волны:
где Условие максимального значения амплитуды стоячей волны: kx = ± np (n = 0, 1, 2, ¼); A = 2x0. (1.147) Условие минимального значения амплитуды стоячей волны: kx = ± (2n + 1)p; A = 0. (1.148) Вектор плотности потока энергии волны – физическая величина, модуль которой равен энергии DE, переносимой волной за единицу времени (Dt=1) через единичную площадку, расположенную перпендикулярно направлению распространения волны (DS^):
где u – плотность энергии в каждой точке среды, среднее значение которой вычисляется по формуле ρ – плотность среды; x0 – амплитуда волны; w - круговая (циклическая частота); v – фазовая скорость (скорость перемещения фазы волны). 1.7. Элементы механики жидкостей Жидкость - агрегатное состояние вещества, промежуточное между твердым и газообразным состояниями. Чистые жидкости по химическому составу - однокомпонентные жидкости. Жидкие смеси (растворы) по химическому составу - двух - или многокомпонентные жидкости. Нормальные (обычные) жидкости - однородные макроскопические и изотропные жидкости. При отсутствии внешних воздействий обладают только одной жидкой фазой. Квантовые жидкости - жидкости, которые могут находиться в нормальной и одной или нескольких анизотропных фазах. Простые жидкости - жидкости, состоящие из сферически симметричных молекул, между которыми действуют силы Ван дер Ваальса, не имеющие какого-либо преимущественного направления и обладающие наиболее простыми свойствами. Ближний порядок - упорядоченное расположение по отношению к любой молекуле ближайших к ней соседей. Зависимость между временем t одного колебания молекулы относительно данного положения и временем " оседлой" жизни t0:
где U - " потенциальный барьер", численно равный разности энергий молекулы в двух возможных областях ее колебаний, разделяющий две возможные области колебаний молекулы); Т - температура жидкости; k - постоянная Больцмана. Число молекул жидкости в некотором сферическом слое толщиной dr на расстоянии r от произвольно выбранной молекулы:
где n0 = N/V - число молекул в единице объема жидкости; F(r) - радиальная функция распределения, которая определяет вероятность нахождения некоторой молекулы жидкости в какой-либо точке ее объема. Вязкость - свойство жидкостей оказывать сопротивление перемещению одной их части относительно другой. Определяется их молекулярным составом и строением. Основной закон вязкого течения (закон Ньютона):
где dv/dz - градиент скорости в направлении z; S - площадь слоя, по которому происходит сдвиг; h - коэффициент динамической вязкости, который характеризует сопротивление жидкости смещению ее слоев. Зависимость коэффициента вязкости жидкостей от температуры:
где U – энергия, необходимая для перехода молекулы жидкости из одного равновесного состояния в другое. Кинематическая вязкость - отношение динамической вязкости к плотности жидкости: n = h/r. (1.154) Текучесть жидкостей – свойство, обратное вязкости, обусловлено той свободой движения молекул в объеме, которая еще допускается силами сцепления между ними. Коэффициент текучести (или текучесть): j = 1/h. (1.155) Сжимаемость - способность жидкости изменять свой объем под действием всестороннего давления. Коэффициент сжимаемости - выражает уменьшение единичного объема (или плотности) при увеличении давления на единицу:
где DV, Dρ - изменение первоначального объема и первоначальной плотности жидкости при изменении давления на Dp. Уравнение состояния жидкости (с определенной степенью точности):
Сфера действия молекулярных сил - область, в которой расположены взаимодействующие молекулы, в центре которой находится рассматриваемая молекула (R ~ 10-9 м). Экспериментальный закон зависимости объема жидкости от температуры: Vt = V0(1 + at), (1.158) где a - коэффициент объемного расширения, который определяется соотношением:
Связь коэффициентов сжимаемости и объемного расширения жидкостей:
Поверхностное натяжение - мера некомпенсированности межмолекулярных сил в поверхностном (межфазном) слое. Работа dA по изменению поверхности жидкости на dS совершается за счет изменения потенциальной энергии поверхностного слоя (поверхностной энергии жидкости) dWps: dA = - dWps = - s× dS, (1.161) где " минус " показывает, что увеличение поверхности жидкости сопровождается совершением работы; s - коэффициент поверхностного натяжения, который характеризует свойства поверхности жидкости и показывает, какую работу необходимо совершить, чтобы увеличить поверхность жидкости на единицу. Работа по изменению поверхности жидкости, совершаемая внешними силами: dA = - F dx = -s× dS = - s× l× dx, (1.162) где l - длина контура, охватывающего поверхность жидкости; dx - смещение границы поверхностного слоя; F - сила поверхностного натяжения; s - коэффициент поверхностного натяжения, который численно равен силе поверхностного натяжения, стремящейся изменить длину контура, охватывающего поверхность жидкости, на единицу. Зависимость коэффициента поверхностного натяжения от температуры:
где r = dQ/dS - количество тепла, затраченное на изменение поверхности пленки на единицу. Полное молекулярное давление в поверхностном слое жидкости: p = p0 ± Dp, (1.164) где p0 - молекулярное давление жидкости с плоской поверхностью; Dp - дополнительное давление, возникающее за счет кривизны поверхности жидкости; знак " +" - соответствует выпуклой поверхности; знак " -" - соответствует вогнутой поверхности. Формула Лапласа для дополнительного давления (для капли, которая полностью заполнена жидкостью, или для пузырька внутри жидкости) в случае: 1) произвольной поверхности
где R1 и R2 - радиусы кривизны поверхностного слоя жидкости; 2) сферической поверхности
где R - радиус сферы; 3) цилиндрической поверхности
где R - радиус цилиндрической поверхности. Формула Лапласа для дополнительного давления (для пузырька, который не заполнен жидкостью, например мыльного) в случае: 1) сферической поверхности
2) цилиндрической поверхности
Условие равновесия капли на поверхности другой жидкости: s12 + s23 = s13, (1.170) где s12 - коэффициент поверхностного натяжения между жидкостью капли и жидкостью, на которой она находится; s13 - коэффициент поверхностного натяжения между жидкостью, на которой находится капля, и воздухом; s23 - коэффициент поверхностного натяжения между жидкостью капли и воздухом. Условие равновесия капли на поверхности твердого тела: s12 + s23× cosq = s13, (1.171) где s12 - коэффициент поверхностного натяжения между жидкостью капли и твердым телом; s13 - коэффициент поверхностного натяжения между твердым телом и воздухом; s23 - коэффициент поверхностного натяжения между жидкостью капли и воздухом; q - краевой угол (угол между касательными к поверхности жидкости и твердого тела). Условие смачивания (краевой угол острый): s12 + s23× cosq £ s13. (1.172) Условие абсолютного смачивания: s12 + s23× cosq< s13. (1.173) Условие несмачивания (краевой угол тупой): s12³ s23× cosq +s13. (1.174) Условие абсолютного несмачивания: s12> s23× cosq +s13. (1.175) Капиллярные явления (капиллярность) - изменение высоты уровня жидкости в узких трубах (капиллярах) или зазорах между двумя стенками. Условие капиллярности: Dp = p, (1.176) где p = rgh - давление;
Высота подъема (опускания) жидкости в капиллярах:
Высота подъема (опускания) жидкости в узком зазоре между погруженными в жидкость параллельными пластинами:
где d - расстояние между пластинами. Давление внутри жидкости во всех точках, расположенных на одном уровне (при механическом равновесии, если жидкость находится в поле тяготения): p = const. (1.179) Давление в жидкости на двух разных уровнях (при механическом равновесии, жидкость находится в поле тяготения) отличается на величину, равную весу вертикального столба жидкости, заключенного между этими уровнями, с площадью сечения, равного единице: p2 = p1 + rgh, (1.180) где p1, p2 - давления жидкости на соответствующих уровнях; h - высота между слоями. Закон Архимеда: на тело, погруженное в жидкость (или газ), находящееся в механическом равновесии, действует выталкивающая сила, равная весу вытесненной телом жидкости (газа), направленная по вертикали вверх и приложенная к центру масс вытесненного объема:
Поток жидкости - совокупность частиц, движущейся жидкости. Линия тока жидкости - линия, касательная к которой совпадает с направлением скорости частицы жидкости в рассматриваемый момент времени и в данной точке пространства. Линии тока жидкости служат для графического отображения потока жидкости. Трубка тока - часть жидкости, ограниченная линиями тока. Установившееся (стационарное) течение жидкости - движение жидкости, при котором форма и расположение линий тока, а также значения скоростей частиц жидкости в каждой их точке не изменяются со временем. Неустановившееся (нестационарное) течение жидкости - движение жидкости, при котором не выполняются условия стационарного движения. Математическая форма записи теоремы (уравнения) о неразрывности (непрерывности струи) для несжимаемой жидкости: S× v = const, (1.182) где S - площадь сечения трубки тока; v - скорость жидкости. Уравнение Бернулли для стационарно текущей идеальной жидкости (для жидкостей с малой вязкостью):
где r - плотность жидкости; v - скорость течения жидкости; h - высота, на которой находится некоторое сечение трубки тока; p - давление жидкости на уровне этих сечений. Закон изменение давления жидкости для двух сечений (с изменением высоты h сечений) при v1 = v2:
Закон изменение давления жидкости для горизонтального потока (h1 = h2):
где p - давление, не зависящее от скорости (статическое давление жидкости);
Полное давление потока жидкости - сумма статического и динамического давлений. Монометрические трубки (трубки Пито) - приборы, с помощью которых измеряют статическое и полное давление жидкости. Скорость течения вязкой жидкости в трубе:
где p1, p2 - давления двух сечений трубы; R - радиус трубы; r - расстояние от центра трубы до рассматриваемой трубки тока; h - коэффициент вязкости жидкости; l - расстояние между сечениями трубы. Формула Пуазейля для определения объема жидкости, прошедшего через сечения трубы:
Ламинарное (слоистое) течение жидкости – когда жидкость как бы разделяется на слои, скользящие относительно друг друга, не перемешиваясь. Ламинарное течение жидкости стационарно. Турбулентное течение жидкости – когда происходит энергичное перемешивание жидкости. При турбулентном течении скорость частиц в каждом месте изменяется хаотично, течение - нестационарное. Число Рейнольдса определяет характер течения жидкости:
где r - плотность жидкости; v - средняя по сечению скорость движения жидкости; l - характерный для поперечного сечения размер; h - динамическая вязкость; n - кинематическая вязкость. 1. 8. Основы теории относительности Теория относительности - физическая теория, рассматривающая пространственно-временные закономерности, справедливые для любых физических процессов (свойства пространства-времени). Специальная (частная) теория относительности (СТО) изучает свойства пространства-времени, справедливые с той точностью, с какой можно пренебрегать действием тяготения. Общая теория относительности (ОТО) - теория тяготения, изучающая свойства пространства-времени, которые определяются действующими полями тяготения. Симметрия (инвариантность) законов физики - неизменность законов физики, устанавливающих соотношение между величинами, характеризующими физическую систему, или определяющие изменение этих величин со временем при определенных операциях - преобразованиях. Преобразования пространства-времени: а) Перенос (сдвиг) системы как целого в пространстве - эквивалентность всех точек пространства, т.е. отсутствие в нем выделенных точек (однородность пространства). Любой физический закон (процесс) происходит одинаково в любой точке пространства. б) Поворот системы как целого в пространстве - симметрия физических законов относительно этого преобразования означает эквивалентность всех направлений в пространстве (изотропию пространства). в) Изменение начала отсчета времени (сдвиг во времени) означает, что физические законы не меняются со временем. г) Переход к системе отсчета, движущейся относительно данной системы с постоянной (по направлению и величине) скоростью означает эквивалентность всех инерциальных систем отсчета. Точечное событие - нечто, происходящее в данной точке пространства в данный момент времени (например, выстрел, распад элементарной частицы). Первый постулат специальной теории относительности (принцип относительности): никакие физические опыты (механические, оптические, тепловые, электромагнитные и т.д.), производимые внутри инерциальной системы отсчета, не позволяют установить, находится ли она в равномерном абсолютном и прямолинейном движении или нет. Второй постулат специальной теории относительности (принцип независимости и постоянства скорости света): скорость света в вакууме одинакова во всех направлениях и не зависит от движения источника света. Третий постулат специальной теории относительности (принцип одновременности событий): события, одновременные в одной системе отсчета, не являются одновременными в другой системе отсчета, то есть одновременность является понятием относительным. " Мир" - четырехмерное пространство, в котором каждое мгновенное событие характеризуется точкой (мировой точкой) с указанием координат. Мировая линия данной материальной точки - некоторая линия в четырехмерном пространстве, отображающая события, происходящие с материальной точкой. Положение материальной точки, тела в четырехмерной системе отсчета задается с помощью координат: x, у, z, и t (x, у, z, - пространственные координаты; t - координата времени, равная: t = ict, где Четырехмерный радиус-вектор S = S (x1, x2, x3, x4) - вектор, проведенный из начала координат в мировую точку. Его три проекции на оси x1, x2 и x3 представляют собой обычные координаты материальной точки x, у и z в момент времени Четырехмерное перемещение D S - вектор, проведенный из начального положения материальной точки в конечное. Первые три проекции этого вектора Dx, Dу, Dz отображают перемещение материальной точки в обычном пространстве, а четвертая проекция, деленная на ic, равна Dt. Пространственно-временной интервал между двумя событиями - расстояние между двумя точками (событиями) в четырехмерном пространстве:
Бесконечно-малый промежуток времени между двумя событиями dt - время, которое отметят часы, находящиеся на теле, в то время как часы системы, по отношению к которой тело движется со скоростью v, отметят время dt:
где b = v2/c2. Скорость в четырехмерной системе отсчета - четырехмерный вектор, первые три проекции которого в
Ускорение в четырехмерной системе отсчета:
Кинематические уравнения движения в четырехмерном системе отсчета (по известному а (t) можно найти v (t) и S (t)):
Формулы преобразования координат при переходе из одной системы отсчета в другую (преобразования Г.А. Лоренца): а) обратные б) прямые Следствия из преобразований Лоренца: а) Закон сложения скоростей (в частном случае, когда скорость " u" направлена вдоль оси OX):
б) Сокращение продольных движущихся масштабов длин (лоренцево сокращение):
где l0 - длина стержня в той системе отсчета, в которой он покоится; l - длина стержня в системе отсчета, движущейся относительно стержня. t1' = t2'. в) Замедление хода движущихся часов:
где τ 0 = t2' - t1' - промежуток времени, прошедший между этими событиями, в подвижной системе К'; τ = t2 - t1 - промежуток времени, прошедший между этими событиями, в неподвижной системе К. Первый закон Ньютона в специальной теории относительности устанавливает существование в природе систем отсчета, сколь угодно близких к инерциальным системам отсчета. Такими системами отсчета являются те, в которых свободное тело не имеет по отношению к ним ускорения. Зависимость массы от скорости:
где m - масса движущегося тела; m0 - масса покоя.
|

 , (1.113)
, (1.113) . (1.116)
. (1.116) . (1.117)
. (1.117)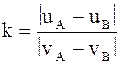 . (1.118)
. (1.118) . (1.119)
. (1.119) ; (1.120)
; (1.120)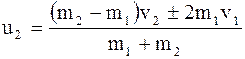 . (1.121)
. (1.121) , а L0 = const. (1.122)
, а L0 = const. (1.122) , (1.123)
, (1.123) . (1.124)
. (1.124) . (1.125)
. (1.125) . (1.126)
. (1.126) . (1.127)
. (1.127)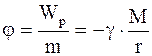 . (1.128)
. (1.128)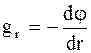 . (1.129)
. (1.129) . (1.130)
. (1.130) . (1.131)
. (1.131) . (1.132)
. (1.132) . (1.133)
. (1.133)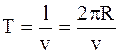 . (1.134)
. (1.134) .
. . (1.135)
. (1.135) , (1.136)
, (1.136) , поперечных -
, поперечных -  , (1.137)
, (1.137) . (1.138)
. (1.138) ;
;  , (1.139)
, (1.139) , (1.140)
, (1.140) . (1.141)
. (1.141) . (1.142)
. (1.142) . (1.143)
. (1.143) . (1.144)
. (1.144)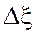
 , (1.145)
, (1.145)
 - оператор Лапласа (лапласиан).
- оператор Лапласа (лапласиан). , (1.146)
, (1.146) - амплитуда стоячей волны.
- амплитуда стоячей волны.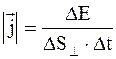 ;
;  = u× v; j = u× v, (1.149)
= u× v; j = u× v, (1.149) ;
; , (1.150)
, (1.150) , (1.151)
, (1.151) , (1.152)
, (1.152) , (1.153)
, (1.153) , (1.156)
, (1.156) . (1.157)
. (1.157) . (1.159)
. (1.159) . (1.160)
. (1.160)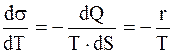 , (1.163)
, (1.163) , (1.165)
, (1.165)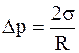 , (1.166)
, (1.166) , (1.167)
, (1.167) ; (1.168)
; (1.168) - дополнительное давление, возникающее за счет кривизны поверхности жидкости при капиллярности;
- дополнительное давление, возникающее за счет кривизны поверхности жидкости при капиллярности; - радиус мениска; r - радиус капилляра; q - краевой угол.
- радиус мениска; r - радиус капилляра; q - краевой угол. . (1.177)
. (1.177) , (1.178)
, (1.178) . (1.181)
. (1.181) , (1.183)
, (1.183) . (1.184)
. (1.184) , (1.185)
, (1.185)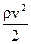 - давление, зависящее от скорости (динамическое давление), которое показывает, на какую величину изменяется статическое давление при остановке движущегося потока жидкости.
- давление, зависящее от скорости (динамическое давление), которое показывает, на какую величину изменяется статическое давление при остановке движущегося потока жидкости.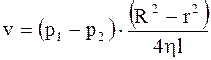 , (1.186)
, (1.186) . (1.187)
. (1.187) ,
, 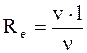 , (1.188)
, (1.188) , c - скорость распространения света в вакууме, t - время). При этом x = x1, у = x2, z = x3, и t = ict = x4.
, c - скорость распространения света в вакууме, t - время). При этом x = x1, у = x2, z = x3, и t = ict = x4. , т.е. в момент времени, которым является четвертая проекция вектора S, деленная на ic.
, т.е. в момент времени, которым является четвертая проекция вектора S, деленная на ic.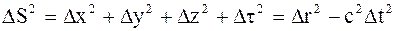 . (1.189)
. (1.189) , (1.190)
, (1.190) отличаются от обычных проекций vx, vу и vz v. Четвертая проекция - мнимая величина, не имеющая физического смысла:
отличаются от обычных проекций vx, vу и vz v. Четвертая проекция - мнимая величина, не имеющая физического смысла: . (1.191)
. (1.191) . (1.192)
. (1.192) ,
,  . (1.193)
. (1.193) ; у = у'; z = z';
; у = у'; z = z';  ; (1.194)
; (1.194) ; у = у'; z = z';
; у = у'; z = z';  . (1.195)
. (1.195) . (1.196)
. (1.196) ;
;  , (1.197)
, (1.197) ;
;  , (1.198)
, (1.198) , (1.199)
, (1.199)


