СИСТЕМА ДАННЫХ
Исходная система I определяет нулевой уровень системологического анализа объекта, как комплекса систем IC, IК, IА. На нулевом уровне конкретизируется значение полного параметра базирования: W Í W1 ´ W2 ´... ´ Wm = {(w1; w2;... wm)}, формируется описание полного состояния переменных: V Í V1 ´ V2 ´... ´ Vn = {(v1; v2;... vn)}. Исходная система в итоге имеет вид (по определению): опр I = (V, W) Û D0. По сути определено множество элементов по переменным и базам, образующих начальную систему данных наблюдений (D0). Для формирования системы данных необходимо выделить отношения вида W ® V, т.е. упорядочить систему I, задав это отношение d: W ® V, d Î D. (6.6.) Упорядоченная система по d называется системой данных: D = (V, W, d) = (I, d), (6.7.) где (V, W) - элементы системы; d - отношения между элементами. Система данных D порождается субъектом заданием отношения d. Выше приведено формальное определение системы данных. Для систем данных, связанных с семантическими операциями (с семантикой), область описания D расширяется за счет включения в систему соответствующих правил вывода: Ds = (S, d), (6.8) где Ds - система данных с семантикой. Методологически системы данных могут быть организованы как нейтральные или направленные системы, с семантикой или без нее: D, Ds, Для нечетких каналов наблюдений в систему данных вводится мера нечеткости: рi: Vi ® [0, 1], i Î Nn , где рi = П рi (р1; р2;...рi;...рn). å рi = 1; 0 £ рi £ 1. Нечеткость определяется как семантика модальности (возможно, вероятно, доверительно...). Нечеткости описываются функциями, задаваемыми на универсальном отрезке (универсуме):
p = (р1; р2; …рn) Î V; р Î [0; 1]. Классы нечетких мер можно определить в виде отношений на универсуме " С" из понятий, определяемых в виде системы высказываний: С - универсум класса нечетких мер; X1 Ì С - меры правдоподобия; X2 Ì С - меры доверия (убежденности); С = X1 È Х2; Х1 Ç Х2 ¹ Æ. Х1 Ç Х2 = Р - вероятностные меры; Х3 - возможностные меры: X3 Ì X1; Х4 - четкая возможность: X4 Ì X3; Х5 - меры необходимости: X5 Ì X2; Хб - четкая необходимость (уверенность): X6 Ì X5; Общая система отношений имеет вид: X6 Ì X5 Ì X2 Ì C = X1 È Х2; X4 Ì X3 Ì X1 Ì C; X1 Ç Х2 = P. Упражнения 1. Постройте диаграмму Эйлера для классов нечетких мер. 2. Определите систему данных в задачах, задавшись понятием " исходная система": а) два сигнала; б) учебный процесс; в) G/G/3/3.
|

 ,
,  .
.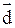 : W®
: W®  , w Î W,
, w Î W, 


