Расчет складских площадей при неравномерном поступлении грузов
При неравномерном поступлении сырья и материалов на склад полезная площадь определяется по формуле минимума суммарных затрат: Sрез.*S1 + 365*Pk*S2®min, где Sрез. – резервная площадь, м2; S1 – затраты на содержание 1 м2 резервной площади, руб.; Рк – вероятность отказа в приемке материальных ресурсов; S2 – потери за каждый день отказа в приемке груза, руб.
Емкость склада определяется: Е=Sпол*qдоп, где qдоп – удельная нагрузка на 1 м2 площади, т/м2.
Средний срок хранения грузов на складе
где
Коэффициент использования емкости склада:
где Е – емкость склада, т; Т – период работы склада, дней.
Оборот склада (Оскл) определяется:
Пропускная способность склада (Пскл): Пскл=Е*Оскл.
Для совершенствования деятельности материально-технического снабжения и складского хозяйства применяется теория массового обслуживания (ТМО). ТМО – раздел математики, изучающий системы, предназначенные для обслуживания массового потока требований случайного характера. Введем обозначения: Заявка (требование) – это обслуживаемый объект; Обслуживающие устройства – это средства, обслуживающие требования; Обслуживающая система – это совокупность обслуживающих устройств. Основная задача ТМО – изучение режима функционирования обслуживающей системы и исследование явлений, возникающих в процессе обслуживания. Одной из характеристик обслуживающей системы является время пребывания требований в очереди. Это время может быть уменьшено за счет увеличения дополнительного количества обслуживающих устройств, но на их установку (приобретение) нужны значительные финансовые вложения. Поэтому с помощью ТМО решаются задачи на экстремум: как достичь определенного уровня обслуживания (максимальное сокращение очереди) при минимальных потерях, связанных с простоем обслуживающих устройств. В области материально-технического снабжения ТМО используется при проектировании и эксплуатации крупных высокомеханизированных баз материально-технического снабжения. С помощью ТМО можно определить площадь складских помещений, которые рассматриваются как обслуживающие устройства, а прибытие транспортных средств (вагонов, автомашин и т.п.) под выгрузку – как требования. Одним из основных элементов ТМО является входной поток требований, который изучается с целью установления его закономерностей и дальнейшего улучшения качества обслуживания. В большинстве случаев входной поток требований – случайная величина. Случайной величиной является и интервал времени между соседними поступлениями требований. Наиболее полно разработан математический аппарат для простейшего потока заявок. Поток заявок является простейшим, если он обладает следующими свойствами: 1. Стационарностью, т.е. вероятность появления того или иного числа заявок на отрезке времени t определяется только длиной этого отрезка (не зависит от того, где именно находится этот участок на оси времени); 2. Ординарностью, т.е. в каждый данный момент времени появляется только одна заявка; 3. Отсутствие последствий, т.е. все заявки приходят в систему независимо друг от друга. Такой поток называется еще «пуассоновский», т.к. количество заявок m, приходящихся на отрезок времени t распределено по закону Пуассона:
где l - плотность потока заявок, т.е. количество заявок в единицу времени; e – основание натурального логарифма; Рm(t) – вероятность того, что в обслуживающую систему за время t поступит именно m требований. Простейший (пуассоновский) поток показывает, что интервалы времени между событиями в потоках имеют показательное распределение с параметром, равным интенсивности потока. Под потоком обслуживания понимается поток заявок, обслуживаемых одним непрерывно занятым обслуживающим устройством. Этот поток оказывается простейшим, только если время обслуживания заявки (Тобс) представляет собой случайную величину, имеющую показательное распределение. Параметр этого распределения – величина, обратная среднему времени обслуживания (интенсивность обслуживания в час - m).
где Тобс – среднее время обслуживания одного требования одним обслуживающим устройством (ч). При нескольких обслуживающих устройствах
где n – количество обслуживающих устройств. Важным параметром складов и баз материально-технического снабжения является коэффициент загрузки a, который определяется как отношение интенсивности поступления требований l к интенсивности обслуживания m.
Количество обслуживающих устройств n должно быть не менее a. В противном случае очередь будет непрерывно расти. Вероятность того, что все обслуживающие устройства свободны:
Вероятность того, что все обслуживающие устройства заняты:
Формула Эрланга для расчета вероятности отказа:
где Рк – вероятность состояния системы ( Р0 – вероятность того, что все аппараты обслуживания свободны; Р1 – вероятность того, что занят один аппарат; Р2 – вероятность того, что заняты 2 аппарата; Рк – вероятность того, что заняты к аппаратов; Рn – вероятность того, что занятые все n аппаратов. Среднее число устройств, свободных от обслуживания:
Коэффициент простоя обслуживающих устройств:
Среднее число устройств, занятых обслуживанием:
Коэффициент загрузки системы:
Средняя длина очереди:
Среднее время ожидания требования в очереди:
Пример. Отгрузка продукции производится с четырех погрузочных площадок. Груз со склада выдается с 8 до 20 часов ежедневно. В день в среднем обслуживается 24 машины. Среднее время погрузки 30 мин. Определить характеристики обслуживания (l, m, Рm(t), Рк). Решение. В рассматриваемом примере склад является системой массового обслуживания; погрузочная площадка, оборудованная соответствующими средства механизации – обслуживающее устройство; автомашины, прибывающие на склад за грузом – поток заявок; погрузка автомашин – обслуживание. Примем, что поток заявок является простейшим. Тогда: 1) l=24 машины/12 часов = 2 заявки в час 2) m=1/0, 5 ч = 2 машины в час 3) a=l/m = 2/2 = 1 Вероятность того, что в течение (t=1) часа на склад прибудут 0; 1; 2; 3; и т.д. автомашины составит:
Расчет показывает, что наиболее вероятен приход на склад 1 и 2 заявок в течение 1 часа; высока вероятность прихода 3 заявок, а вероятность прибытия на склад 4 и более заявок весьма низка; часто вообще отсутствие заявок. По формуле Эрланга определим вероятность состояния системы при наличии n=0, 1, 2, 3, 4 площадок.
Из расчета видно, что вероятность получить отказ в системе обслуживания низка – всего 15 %. Однако в то же время все 4 площадки почти 37 % своего времени будут пустовать в ожидании автомашины.
|

 ,
, - общее количество тонно-дней хранения за период;
- общее количество тонно-дней хранения за период; - общее количество груза, прошедшего через склад.
- общее количество груза, прошедшего через склад. ,
, или
или  или
или 
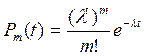 , e =2, 75
, e =2, 75 ,
, ,
, ; если
; если  , то a=l*Тобс
, то a=l*Тобс

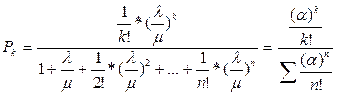 ,
, );
); .
.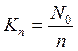 .
. .
. .
. .
. .
. .
. ;
; 
 ;
; 
 ;
; 
 ;
;  .
. ;
; ;
;  ;
;  ;
; ;
;  .
.


